1、电动机工作的物理原理
1.1 麦克斯韦方程组
电动机是不断转换电磁能和机械能的换能器。
当输入电能时,电动机可以连续输出扭矩和机械能。
即,电动机;反之,如果有外力不断推动电动机轴并输入机械能,电动机就可以从线端反向连续输出电压和电能,即发电机。
历史上,静态变压器也被算作电动机,但逐渐演变为专指电动机和发电机。
电动机的优点之一是损耗相对较小,因此效率较高。
大型电动机的效率高达 99%。

说到电磁系统,就不可避免地要提到麦克斯韦方程组。
在宏观世界乃至微观世界,
麦克斯韦方程组可以非常有效地描述系统特性。
麦克斯韦方程组是从以前对电磁现象的研究中总结出来的。
有四个非常基本的方程,有微分形式和积分形式。
现在让我们以积分形式研究麦克斯韦方程组。
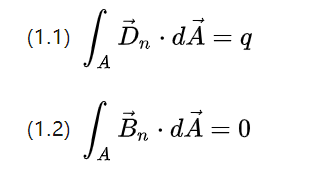
上述两个方程分别描述了封闭空间表面内场密度的磁通、流出电势位移图的总和以及旋转磁场感应图的总和
根据高中学过的知识,点电荷激励可以产生电场,磁场不能由磁单极子激励,而是要延长封闭的路径,所以电场是活跃的,磁场是被动的。
因此总电势位移通量为总电荷 q,总磁通量为 0。
上述两个方程描述了场强的自旋量、总电场强度和总磁场强度的积分。
分别对应于沿着闭合空间曲线上的曲线路径转动一圈的磁通量的变化率和电势位移(电流强度)的变化率。
高斯和斯托克斯公式还允许将上述四个方程重写为微分形式,如下所示。
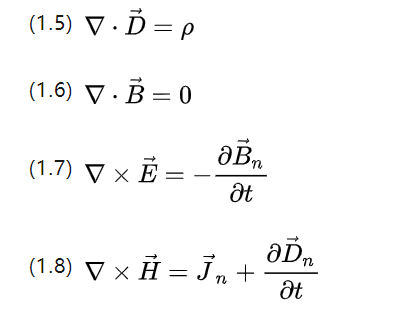
▽ 对于Nabla算子,用向量点积计算散射,用叉积计算自旋,P为电荷体密度,Jn为电流密度。
上述方程基本上可以描述所有交流感应电机系统中发生的所有电磁行为
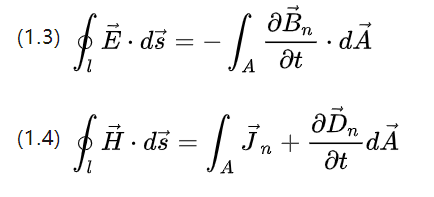
1.2 电能的材料极化和磁化
在施加的旋转磁场中,材料分子将改变其方向,因为极性受到场强的影响。
原来由大小不等排列的分子团形成的电畴,会因外加磁场而发生极化,电荷分布方向趋于收敛。
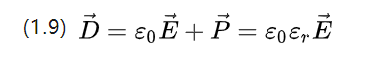
E0=8.854187817*10-12F/m为真空介电常数,也就是真空介电常数,P为相对介电常数,由材料本身的性质决定。
式(1.9)描述了所施加电场的电势位移密度和相应的偏振强度图。
在外加磁场中,用同样的方法可以得到相应的磁畴和磁化强度。
与电场不同的是,引入了磁极化强度M,它描述了材料的磁感应强度与真空环境的磁感应强度之间的差异。
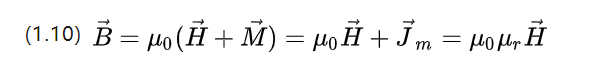
U0=4π*10-7 N.A-2是真空磁导率,Ur是相对磁导率,描述了材料允许磁场通过的能力。
如果你<=1是抗磁的,该材料阻止磁场通过;如果图像是顺磁性的,则该材料会顺应磁场的通过。
如果你>=1o 5 具有铁磁性,钴镍铁等材料磁化后会增强磁场。去除磁场后仍保留一定强度的磁场,称为剩磁。
电机运行过程中会不断地磁化和退磁,因此还应注意检查不同材料的磁滞线。
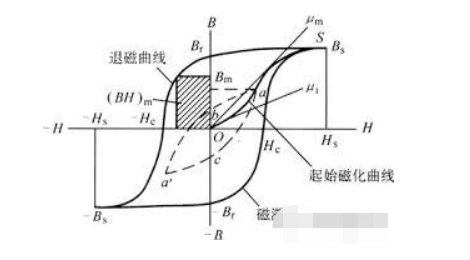
磁滞线描述了在强度为 H 的外加磁场作用下,磁性材料的磁感应强度随着场强的增加而增加。
这种磁感应强度在达到磁饱和后并不跟随磁场强度。
达到磁饱和后,很难跟随场强的增加。当外部磁场强度缓慢减小到零时,可以看出退磁曲线在经过零点时仍然保留着剩磁B。
这种剩磁显示了制造永磁体的一般原理,即定向磁化,然后逐渐退磁。当施加反向磁场时,磁感应强度为零甚至相反方向增加,这种多余的量称为矫顽力H。
1.3 电磁力和机械能
电机最大的价值在于实现电能向机械能的转换,对外做功,执行目标运动。
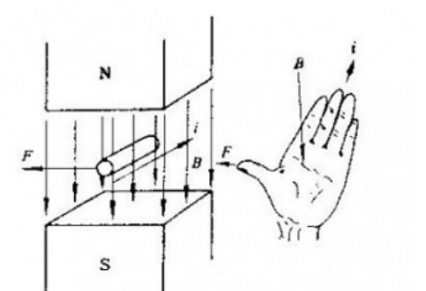
带电粒子在磁场中的运动受到垂直于运动方向的洛伦兹力的作用,其宏观表达式为安培力 Hm = Il * B ,可以用左手定则来判断方向,
I是导体在磁场中沿电流方向的有效长度。
静电场Fe=qE中也存在相应的电场力。
而磁场和电场本身都是场,施加在其中的电荷或电流元素上的力取决于体积和场密度,因此可以用场来考察相应的场力。
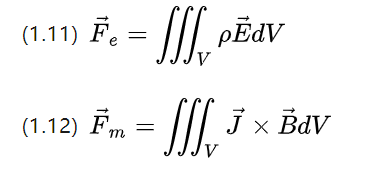
上述两个方程仍然保持对称性,一定体积内的电荷密度P由于电场场强而产生电力密度fe=pE,
一定体积内的电流密度J由于磁场强度而产生磁力密度Fm=J*B(在各向同性材料和恒定电流的情况下必须使用上式(1.12))。
这个表达式启发我们直接考察电磁场的能量和能量密度。
这样,通过求梯度就可以确定某一点的电磁势能,从而得到相应的电磁力密度,从而求出被测物体所受的总电磁力。
1.4 线圈模型
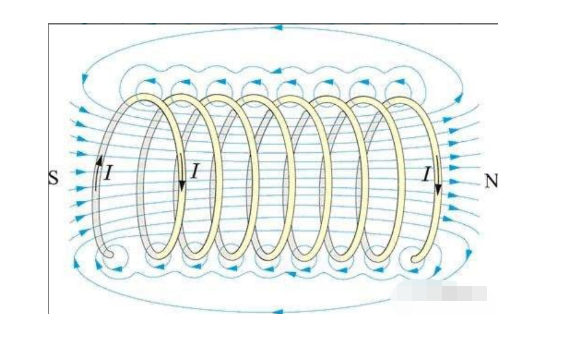
线圈是形成感应电机模型的基本元件,连接着交流电机的电路模型和物体的物理模型。
通电导体的直线部分在其周围产生环形磁场(根据方程 1.4)。
当导体首尾闭合时,环形磁场在导体环中心形成垂直穿过导体环的磁力线,例如螺线管。
仅考虑通电导体上的电流,(1.4) 简化为:
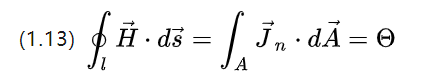
磁动势 (magnetische Durchfluchtung) 是激励场强度的来源,本质上是通过一段闭合导体的总电流的强度,单位为 [A]。
由于实际上通电的电线将缠绕成线圈,因此电线电流被离散化,并且(1.13)被重写为
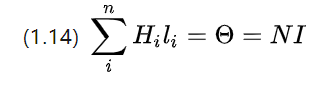
N是线圈的总匝数,即匝数。
可见,匝数越多,总电流越大,磁势越高,能激发的磁场越强。
单匝线圈在时变磁场中会在导线两端感应出电压,这种现象如(1.3)所描述。
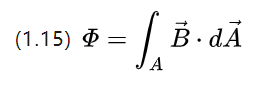
可以理解,磁感应强度也可以理解为磁通密度,将其代入(1.3)即可得到
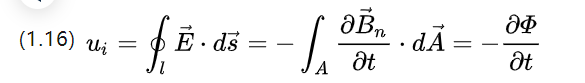
Ui为感应电势,考虑磁通变化的两种形式,一种是改变线圈面积而改变磁通密度,则有:
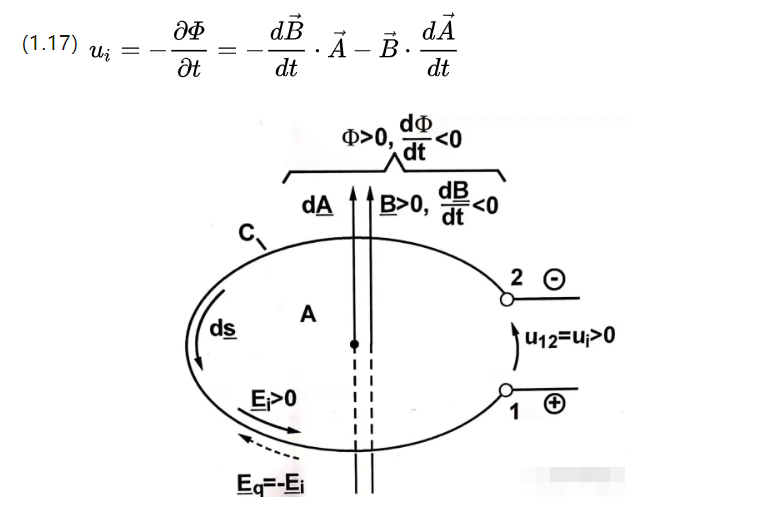
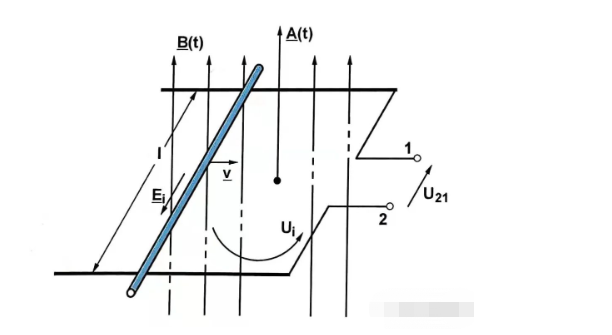
前一部分是形式变换的感应势,后一部分是平移变换的感应势。
前者具有随时间变化的磁通密度,而后者具有随时间变化的有效线圈面积。
这个归纳原理在高中物理中提到过,也被称为笛子定理。
当线圈有很多匝数时,总有效磁通恰好是展开的线圈匝数的整数倍,从而引入磁链的概念。
链的定义如下图所示。
请注意,磁链是一个标量,就像磁通量一样。由于电流本身的变化也会引起磁通的变化,因此趋势是阻碍磁通变化,可以定义为:
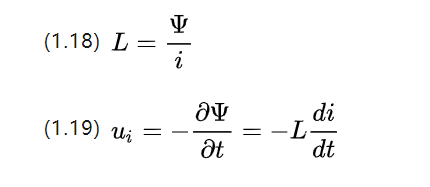
i是变化的电流强度,L是以亨利[H]为单位的自感系数,其大小与线圈体积形状、匝数和磁导率有关。
感应电动机中的线圈是在线圈中间置有铁磁材料,如铁芯,以增加磁导率,使线圈绕在铁芯上,故名绕组。
对于一段线性均质材料,其自感系数可以用下式近似
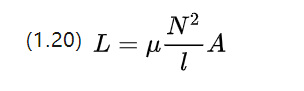
自感是线圈自身电流变化而感应出抑制电压的现象,它对直流电动机的电流变化具有阻碍作用。
当两个线圈相互靠近时,除了自身的自感外,还因为相邻线圈上的电流变化而产生互感
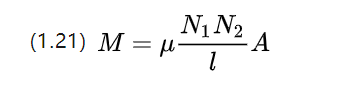
具有线性恒等式的材料的互感系数由上式近似,可知互感同时受到两个线圈匝数的影响。
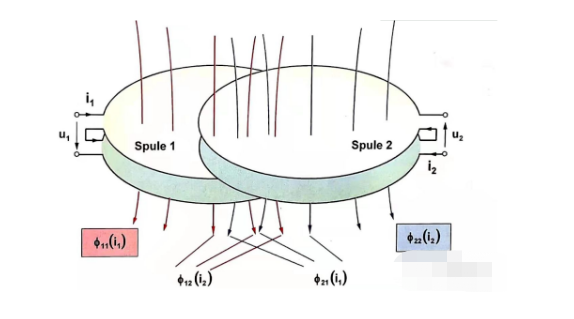
忽略电阻并检查两个相邻线圈的自感和互感,直流电机的电压方程可由图 1.5 列出
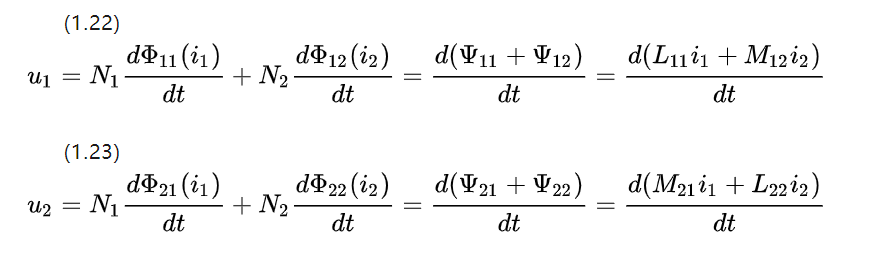
由于耦合部件具有相同的材料参数和形状,因此得到的互感系数相等M12=M21。
因此,每个线圈上的耦合链的大小与直流电机相应转子绕组线圈上的电流强度成正比。
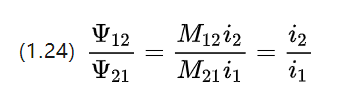
1.5 电能和磁路的欧姆定理
中学时我们学习了欧姆定理,该定理指出导体的电阻是两端电压与电流的比值,并且有一个公式来描述电阻材料本身。
Q,即电导率,恰好是电阻率 P 的倒数,描述传导电流的能力。
除了施加电阻外,还可以使用电动机工作时的电导率图来描述电压和电流之间的关系。
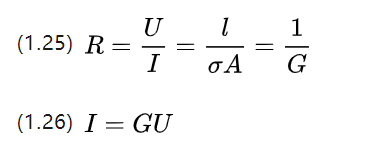
现在检查单位面积的电流强度,即电流密度 J = I/A e(e 是单位矢量),其中电流密度作为指向交流电机电流方向的矢量。
这可以与电压方程 U=E.l 和 (1.25) 结合起来,将 (1.26) 重写为
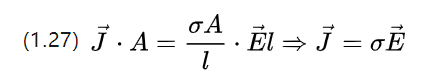
上式描述了微观层面的欧姆定理,即电流密度的变化对应于施加到导体上的恒定场强。
Lm是磁通通过一段磁路的有效长度,A是相应的磁通面积。
上式与电阻公式非常相似。
我们把磁阻公式再变形一下,可以继续得到
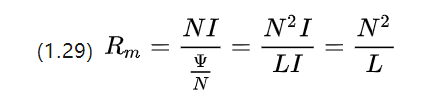
可以看出,单位内的磁阻实际上是电感系数的倒数。
继续类比电导的概念,我们得到磁导A(magnetische Leitwert,单位为[H]或[Ωs])
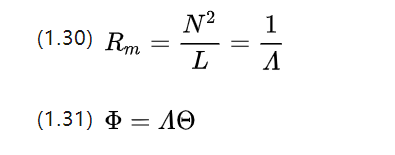
在电路中我们求出(1.26)的微分元,得到微观欧姆定理,那么磁路对应的微观欧姆定理是什么呢?
我们可以继续重写方程(1.31),注意到磁通量本身具有磁通密度 B ,然后得出
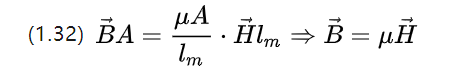
所以微观磁路欧姆定理为式(1.10),其下的磁场强度就是恒定磁场磁化得到的磁通密度。
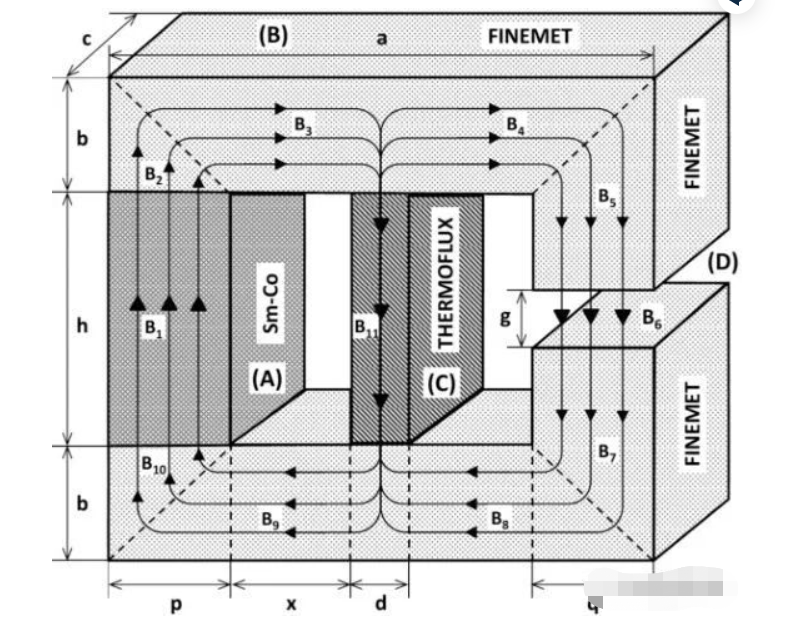
通过磁阻的计算分析,可以实现对整个电机绕组磁极、铁芯部分和中间气隙部分磁通的微元分析,从而可以实现离散有限元分析FEM(Finite-Elemente-Methode)整个磁路。
磁路中的电路也可以应用基尔霍夫定理,非常直观方便。
欢迎在评论区与我们分享更多关于电机的资讯!
任何关于电机的咨询,请联系专业电机 制造商 在 中国 如下:

东淳电机拥有广泛的电机产品,应用于交通、基础设施、建筑等各个行业。
获得及时回复。








