Fysiska grunder för elmotorer

1. Den fysiska principen för elmotorarbete

1.1 Maxwells ekvationssystem

Elmotorn är en givare som ständigt omvandlar elektromagnetisk energi och mekanisk energi.

När elektrisk energi matas in kan elmotorn kontinuerligt mata ut vridmoment och mekanisk energi.

dvs den elektriska motorn; omvänt, om en yttre kraft kontinuerligt trycker på elmotoraxeln och matar in mekanisk energi, kan elmotorn kontinuerligt mata ut spänning och elektrisk energi från trådänden i omvänd riktning, dvs. generatorn.

Historiskt sett har den statiska transformatorn också räknats som en elmotor, men den utvecklades gradvis till att uteslutande avse elmotorer och generatorer.

En av fördelarna med elmotorer är att deras förluster är relativt små, så de uppnår hög verkningsgrad.

Stora elmotorer kan uppnå verkningsgrader på upp till 99 %.

När man talar om elektromagnetiska system är Maxwells ekvationssystem oundvikligt.

I den makroskopiska världen och till och med i den mikroskopiska världen,

Maxwells ekvationssystem kan användas mycket effektivt för att beskriva systemegenskaperna.

Maxwells ekvationssystem har sammanfattats från tidigare studier av elektromagnetiska fenomen.

Det finns fyra mycket grundläggande ekvationer, både i differential- och integralform.

Låt oss nu undersöka Maxwells ekvationssystem i integralform.

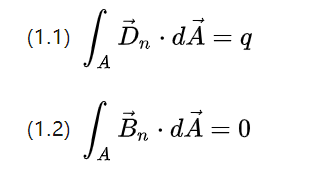
Ovanstående två ekvationer beskriver flödet av fälttätheten, summan av utflödespotentialförskjutningsbilden respektive summan av den roterande magnetfältsinduktionsbilden i en sluten rymdyta

Enligt de kunskaper man lärde sig i gymnasiet kan det elektriska fältet genereras genom punktladdningsexcitering, magnetfältet kan inte exciteras av den magnetiska monopolen, men för att förlänga vägen stängd, så att det elektriska fältet är aktivt, är magnetfältet passiv.

Så det totala potentiella skiftflödet är den totala laddningen q och det totala magnetiska flödet är 0.

Ovanstående två ekvationer beskriver spinnstorheterna för fältintensiteten, integralerna av den totala elektriska fältintensiteten och den totala magnetfältsintensiteten.

Motsvarande ändringshastigheten för det magnetiska flödet och ändringshastigheten för potentialförskjutningen (strömintensitet), respektive, för ett varv längs kurvans bana på en sluten rymdkurva.

Gauss och Stokes formler tillåter också omskrivning av ovanstående fyra ekvationer till differentialform enligt följande.

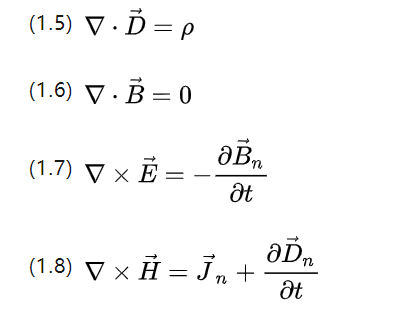
▽ för Nabla-operatorn, med vektorpunktsprodukt för att beräkna spridningen och gaffelprodukten för att beräkna spinn, P för laddningskroppens densitet och Jn för strömdensiteten.

Ovanstående ekvationer kan beskriva i princip allt elektromagnetiskt beteende som förekommer i alla AC-induktionsmotorsystem

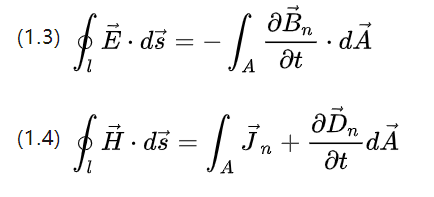
1.2 Materialpolarisering och magnetisering för elektrisk energi

I ett applicerat elektriskt roterande magnetfält kommer materialmolekylerna att ändra sin orientering eftersom polariteten påverkas av fältstyrkan.

De elektriska domänerna som bildas av de ursprungliga ojämnt arrangerade molekylgrupperna av olika storlekar kommer att polariseras på grund av det applicerade magnetfältet, och laddningsfördelningsorienteringen konvergerar.

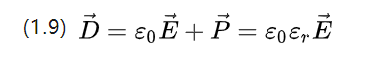
E0=8,854187817*10-12F/m är vakuumpermittiviteten, som också är vakuumdielektricitetskonstanten, och P är den relativa dielektricitetskonstanten, som bestäms av materialets egenskaper.

(1.9) beskriver den potentiella skifttätheten för det pålagda elektriska fältet och motsvarande bild av polarisationsintensiteten tillsammans.

I ett applicerat magnetfält kan motsvarande magnetiska domäner och magnetiseringsstyrkor erhållas på samma sätt.

Till skillnad från det elektriska fältet introduceras en magnetisk polarisationsstyrka M, som beskriver skillnaden mellan den magnetiska induktionsstyrkan hos materialet och den hos vakuummiljön.

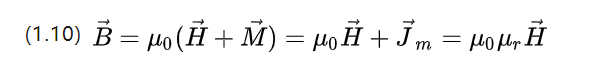
U0=4π*10-7 N.A-2 är vakuumpermeabiliteten och Ur är den relativa permeabiliteten, vilket beskriver materialets förmåga att låta ett magnetfält passera igenom.

Om Ur<=1 är antimagnetiskt, materialet förhindrar passage av ett magnetfält; om bilden är paramagnetisk överensstämmer materialet med passagen av ett magnetfält.

Om Ur>=1o 5 är ferromagnetiskt, materialet såsom ferro-kobolt nickel kommer att förstärka magnetfältet efter magnetisering. Och sedan behålla en viss styrka av magnetfältet efter att ha tagit bort magnetfältet, vilket kallas remanent magnetism.

I processen med motordrift kommer det att finnas konstant magnetisering och avmagnetisering, så uppmärksamhet bör också ägnas åt undersökningen av hystereslinjerna för olika material.

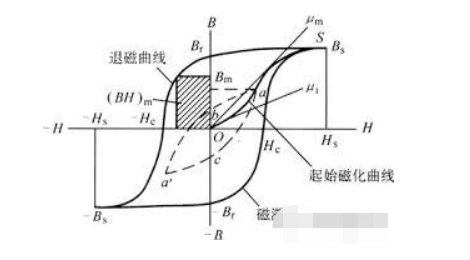
Hystereslinjen beskriver den ökande magnetiska induktionen av ett magnetiskt material när fältstyrkan ökar under inverkan av ett applicerat magnetfält med styrka H.

Denna magnetiska induktion följer inte fältstyrkan efter att ha uppnått magnetisk mättnad.

Efter att den magnetiska mättnaden uppnåtts är det svårt att följa ökningen av fältstyrkan. När den externa magnetiska fältstyrkan långsamt minskar till noll kan man se att avmagnetiseringskurvan fortfarande behåller den remanenta magnetiseringen B när den passerar nollpunkten.

Denna remanenta magnetisering visar den allmänna principen för tillverkning av permanentmagneter, dvs riktningsmagnetisering följt av gradvis avmagnetisering. När det omvända magnetfältet appliceras går den magnetiska induktionsstyrkan till noll eller till och med ökar i motsatt riktning, och detta överskott kallas koerciviteten H.

1.3 Elektromagnetisk kraft och mekanisk energi

Motorns största värde är att realisera omvandlingen av elektrisk energi till mekanisk energi, att utföra arbete externt och att utföra målrörelsen.

Rörelsen av en laddad partikel i ett magnetfält är föremål för Lorentz-kraften vinkelrätt mot rörelseriktningen, vars makroskopiska uttryck är Amperekraften Hm = Il * B , som kan bedömas genom att använda vänsterregeln för att bestämma riktning,

I är den effektiva längden av ledaren i magnetfältet i strömriktningen.

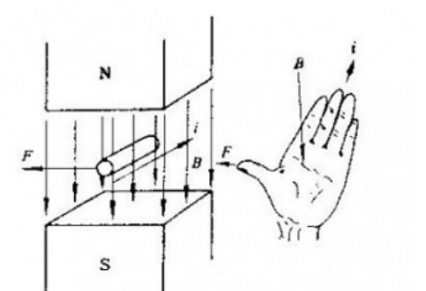
Det finns också en motsvarande elektrisk fältkraft i det elektrostatiska fältet Fe=qE .

Och både magnetiska och elektriska fält är själva fält, och kraften som appliceras på laddningen eller strömelementet i dem beror på volymen och fälttätheten, och därmed kan motsvarande fältkraft undersökas i termer av fältet.

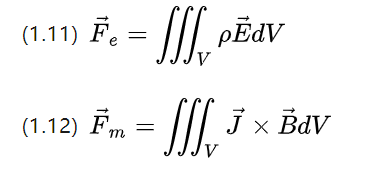
Ovanstående två ekvationer bibehåller fortfarande symmetrin, laddningstätheten P i en viss volym på grund av det elektriska fältets fältstyrka ger den elektriska kraftdensiteten fe = pE,

Strömtätheten J i en viss volym på grund av magnetfältets fältstyrka ger den magnetiska kraftdensiteten Fm = J * B (ekvationen ovan (1.12) måste användas i fallet med isotropa material och konstant ström) .

Detta uttryck inspirerar oss att direkt undersöka det elektromagnetiska fältets energi och energitäthet.

På så sätt kan den elektromagnetiska potentiella energin vid en viss punkt bestämmas genom att hitta gradienten för att erhålla motsvarande elektromagnetiska kraftdensitet och därmed hitta den totala elektromagnetiska kraften på föremålet som undersöks.

1.4 Coil modell

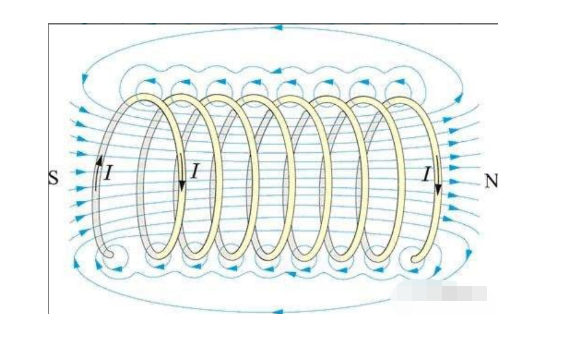
En spole är ett grundläggande element som bildar en modell av induktionsmotorer, som överbryggar kretsmodellen för växelströmsmotorn och den fysiska modellen av objektet.

En rak sektion av spänningssatt ledare genererar ett toroidformat magnetfält runt den (enligt ekvation 1.4).

När ledaren är stängd i början och slutet bildar toroidfältet magnetiska kraftlinjer i mitten av ledarringen som passerar vertikalt genom ledarringen, såsom en solenoid.

Med tanke på endast strömmen på den spänningssatta ledaren, förenklar (1.4) att:

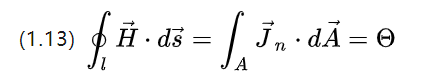
Den magnetomotoriska kraften (magnetische Durchfluchtung), som är källan till styrkan hos excitationsfältet, är i huvudsak styrkan hos den totala ström som passerar genom en sektion av sluten ledare i [A].

Eftersom den spänningssatta ledningen i praktiken kommer att lindas till en spole, diskretiseras trådströmmen och (1.13) skrivs om som

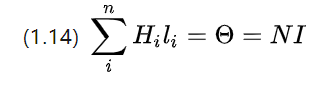
N är det totala antalet lindningar i spolen, dvs antalet varv.

Det kan ses att om antalet varv är högre är den totala strömmen högre, den magnetiska potentialen är högre och ju starkare magnetfältet kan exciteras.

En envarvsspole i ett tidsvarierande magnetfält kommer att inducera en spänning i båda ändarna av tråden, ett fenomen som beskrivs av (1.3).

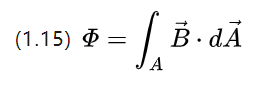
Det kan förstås att den magnetiska induktionen också kan tolkas som den magnetiska flödestätheten, som kan erhållas genom att ersätta (1.3)

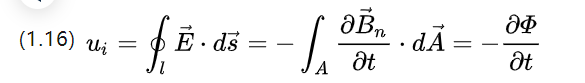
Ui är den inducerade elektriska potentialen, överväg två former av flödesändring, den ena är att ändra spolarean men ändra flödestätheten, sedan finns det följande;

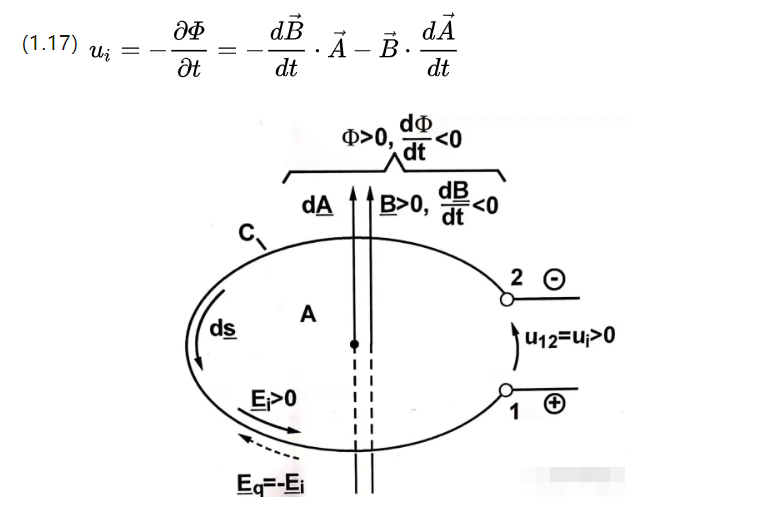
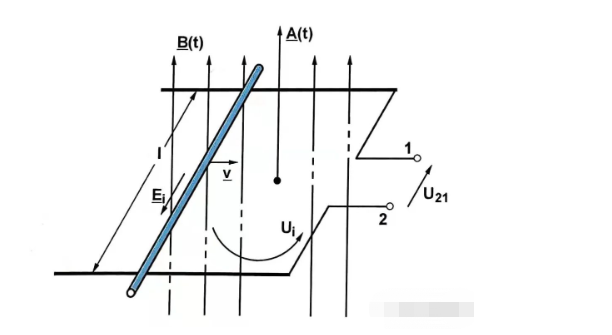
Den förra delen är den formellt transformerade induktionspotentialen (transformationsinducerad spänning) och den senare delen är den translationellt transformerade induktionspotentialen (translationsinducerad spänning).

Den förra har en tidsvarierande magnetisk flödestäthet, medan den senare har en tidsvarierande effektiv spolarea.

Denna induktionsprincip nämns i gymnasiefysik och är även känd som flöjtsatsen.

När en spole har många varv är det totala effektiva flödet exakt en heltalsmultipel av de expanderade spolvarven, vilket introducerar konceptet med en magnetisk kedja.

Kedjan definieras i figuren nedan.

Observera att den magnetiska kedjan är en skalär storhet, precis som det magnetiska flödet. Eftersom en förändring i strömmen i sig också kan orsaka en förändring i flöde, är tendensen att hindra flödesändringen, vilket kan definieras som:

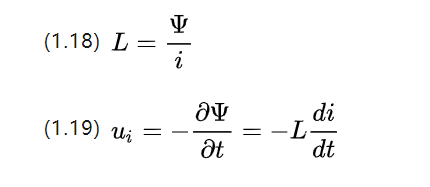
i är den varierande strömintensiteten, L är självinduktanskoefficienten i Henry [H], och dess storlek är relaterad till spolens volymform, antal varv och magnetisk permeabilitet.

Spolar i induktionsmotorer är gjorda för att ha ferromagnetiskt material i mitten av spolen, såsom en järnkärna, för att öka den magnetiska permeabiliteten, så att spolen lindas på järnkärnan, därav namnet lindning.

För en sektion av linjärt homogent material kan dess självinduktanskoefficient approximeras med följande ekvation

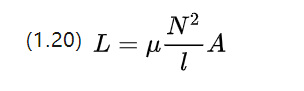
Självinduktans är en spole av sina egna strömförändringar för att inducera fenomenet undertryckningsspänning, dess tendens att hindra strömförändringar i likströmsmotorn.

När två spolar nära varandra, förutom sin egen självinduktans, men också på grund av de intilliggande spolarna på strömförändringar och ömsesidig induktans

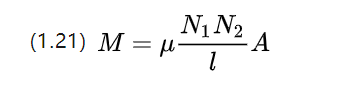
Koefficienten för ömsesidig induktans för material med linjära identiteter approximeras av ovanstående ekvation, som visar att den ömsesidiga induktansen påverkas av antalet varv av de två spolarna samtidigt.

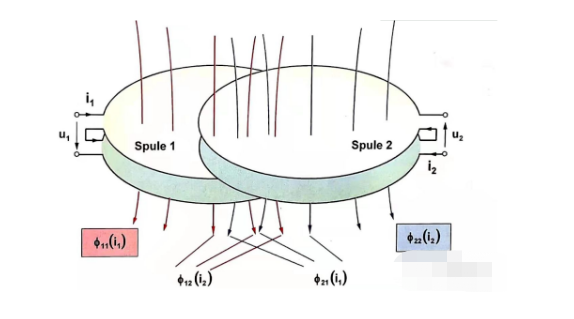
Om man ignorerar resistansen och undersöker själv- och ömsesidig induktans för de två intilliggande spolarna, kan spänningsekvationen listas från figur 1.5 om likströmsmotorer

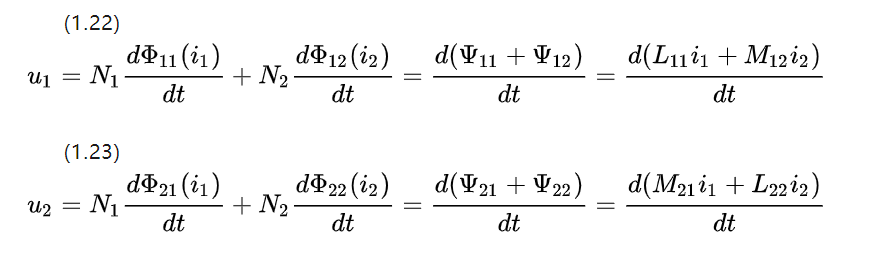
Eftersom kopplingsdelarna har samma materialparametrar och form, är de resulterande ömsesidiga induktanskoefficienterna lika med M12=M21.

Så storleken på kopplingskedjorna på varje spole är proportionell mot strömstyrkan på motsvarande rotorlindningsspole för likströmsmotor.

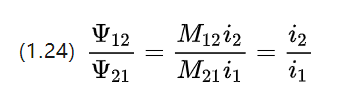
1,5 Ohms sats för elektrisk energi och magnetiska kretsar

På gymnasiet studerade vi Ohms sats, som säger att en ledares resistans är förhållandet mellan spänning och ström i båda ändar, och att det finns en formel för att beskriva själva resistiva materialet.

Q, som är konduktiviteten, som är exakt den reciproka av resistiviteten P och beskriver förmågan att leda ström.

Förutom att applicera motstånd kan förhållandet mellan spänning och ström också beskrivas med hjälp av konduktivitetsbilden när elmotorn fungerar.

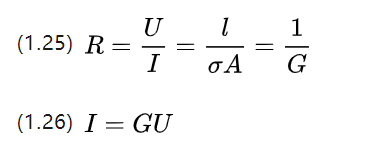
Undersök nu strömintensiteten per ytenhet, d.v.s. strömtäthet J = I/A e (e är enhetsvektorn), med strömtätheten som en vektor som pekar i strömriktningen för växelströmsmotorer.

Detta kan kombineras med spänningsekvationen U=E.l och (1.25) skrivas om (1.26) som

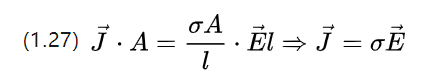
Ovanstående ekvation beskriver Ohms sats på mikroskopisk nivå, d.v.s. variationen av strömtätheten som motsvarar en konstant fältstyrka som appliceras på ledaren.

Lm är den effektiva längden av det magnetiska flödet genom en sektion av den magnetiska kretsen, och A är motsvarande flödesarea.

Ovanstående ekvation är mycket lik motståndsformeln.

Låt oss deformera magnetresistansformeln igen och vi kan fortsätta att erhålla

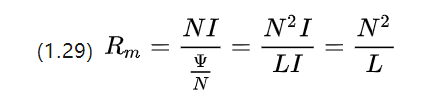
Det kan ses att i enheter är magnetoresistansen faktiskt inversen av induktanskoefficienten.

Om vi fortsätter analogin med begreppet konduktans, får vi den magnetiska konduktansen A (magnetisk Leitwert, i [H] eller [Ωs])

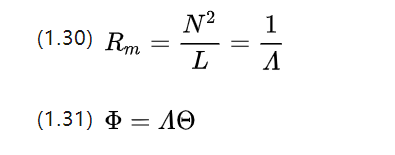
I kretsen hittar vi differentialelementen för (1.26) och får den mikroskopiska Ohms sats, så vad motsvarar den mikroskopiska Ohms sats den magnetiska kretsen?

Vi kan fortsätta med att skriva om ekvation (1.31), och notera att det magnetiska flödet i sig har en flödestäthet B , som sedan ger

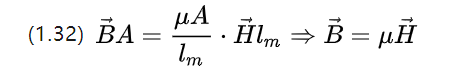
Så den mikroskopiska magnetkretsen Ohms sats är ekvation (1.10), och den magnetiska fältstyrkan under är flödestätheten som erhålls från magnetiseringen av ett konstant magnetfält.

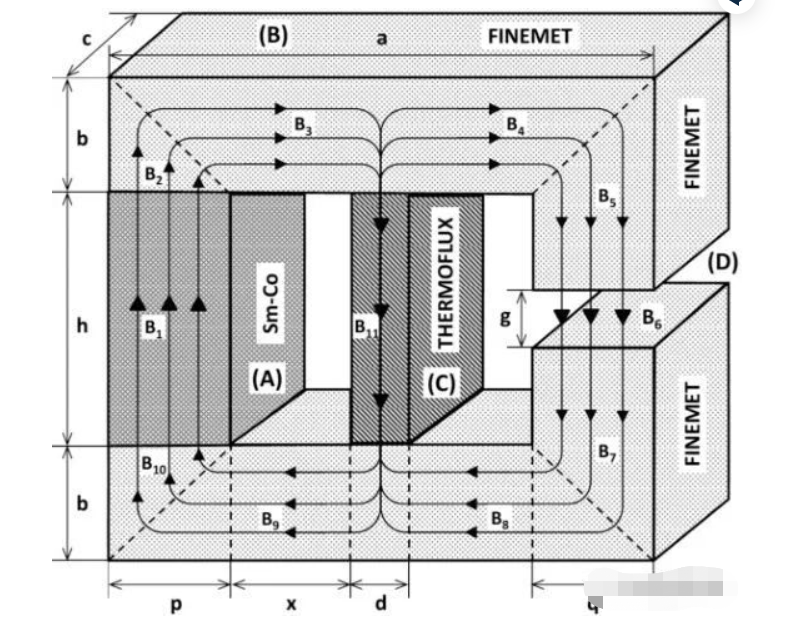
Den beräkningsmässiga analysen av reluktansen kan användas för att realisera en mikroelementanalys av flödet i hela motorlindningspolen, kärndelen och den mellanliggande luftgapsdelen, vilket kan realisera en diskret finita elementanalys FEM (Finite-Elemente-Methode) av hela magnetkretsen.

Det är också möjligt att tillämpa Kirchhoffs teorem för kretsen i den magnetiska kretsen, vilket är mycket intuitivt och bekvämt.

Välkommen att dela med oss av mer information om elmotorer i kommentarsfältet!

Alla frågor om elmotor, vänligen kontakta den professionella elmotorn tillverkare i Kina som följer: