1. 電気モーターの動作の物理原理
1.1 マクスウェル方程式系
電気モーターは、電磁エネルギーと機械エネルギーを常に変換する変換器です。
電気エネルギーが入力されると、電動モーターはトルクと機械エネルギーを継続的に出力できます。
つまり、電気モーターです。逆に、外力が電動機のシャフトを押し続けて機械エネルギーを入力すると、電動機は逆にワイヤの端、つまり発電機から電圧と電気エネルギーを継続的に出力できます。
歴史的には、静止変圧器も電気モーターとして数えられていましたが、徐々に電気モーターと発電機のみを指すように発展しました。
電動機の利点の 1 つは、損失が比較的小さいため、高効率が得られることです。
大型の電気モーターは最大 99% の効率を達成できます。

電磁システムについて語るとき、マクスウェル方程式系は避けられません。
マクロの世界でも、ミクロの世界でも、
マクスウェル方程式系は、システムのプロパティを記述するために非常に効果的に使用できます。
マクスウェル方程式系は、電磁現象に関する以前の研究から要約されています。
非常に基本的な方程式が 4 つあり、微分形式と積分形式の両方があります。
ここで、積分形式のマクスウェル方程式系を調べてみましょう。
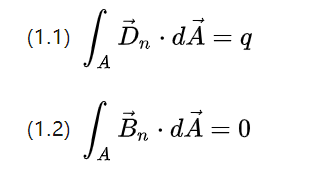
上の 2 つの方程式は、それぞれ磁場密度の磁束、つまり閉じた空間表面における流出電位シフト画像の合計と回転磁場誘導画像の合計を表します。
高校で学んだ知識によると、電場は点電荷励起によって生成でき、磁場は磁気単極子によって励起できませんが、閉じた経路を延長するため、電場はアクティブになり、磁場は受け身。
したがって、ポテンシャルシフト磁束の合計は電荷の合計 q であり、磁束の合計は 0 です。
上の 2 つの方程式は、磁場強度のスピン量、総電場強度の積分、および総磁場強度を記述します。
閉空間曲線上の曲線の経路に沿った 1 回転に対する磁束の変化率と電位シフト (電流の強さ) の変化率に相当します。
ガウスとストークスの公式を使用すると、上記の 4 つの方程式を次のように微分形式に書き直すこともできます。
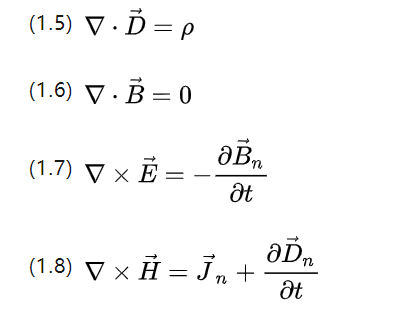
▽ ナブラ演算子用。スキャッタを計算するベクトル内積とスピンを計算するフォーク積、荷電体密度を P、電流密度を Jn とします。
上記の方程式は、基本的にすべての AC 誘導モーター システムで発生するすべての電磁的動作を説明できます。
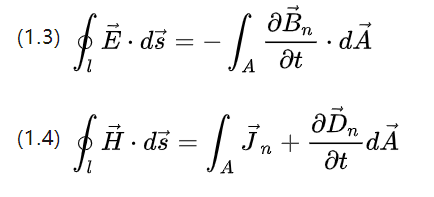
1.2 電気エネルギーにおける物質の分極と磁化
印加された回転電気磁界では、極性が磁界の強さの影響を受けるため、材料分子の配向が変わります。
もともと不均一に配置されたさまざまなサイズの分子群によって形成された電気ドメインは、印加された磁場によって分極され、電荷分布の向きが収束します。
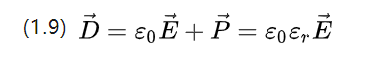
E0=8.854187817*10-12F/m は真空の誘電率であり、真空の誘電率でもあり、P は比誘電率であり、材料自体の特性によって決まります。
(1.9) は、印加された電場の電位シフト密度と、対応する分極強度の画像を一緒に説明します。
磁場を印加すると、対応する磁区と磁化の強さが同じ方法で得られます。
電場とは異なり、材料の磁気誘導強度と真空環境の磁気誘導強度との差を表す磁気分極強度 M が導入されます。
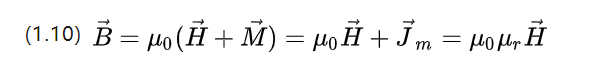
U0=4π*10-7 N.A-2 は真空の透磁率、Ur は磁場を通過させる材料の能力を表す比透磁率です。
イフ・ウル<=1 は反磁性を持ち、材料は磁場の通過を防ぎます。画像が常磁性の場合、その素材は磁場の通過に準拠します。
イフ・ウル>=1o 5 は強磁性であるため、フェロコバルトニッケルなどの材料は磁化後に磁場を強化します。そして、磁場を取り除いても一定の強さの磁場が残ることを残留磁気といいます。
モーターの動作過程では、一定の磁化と減磁が発生するため、さまざまな材料のヒステリシス線の検査にも注意を払う必要があります。
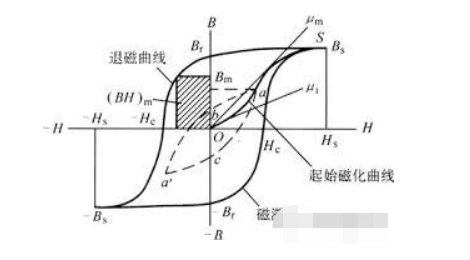
ヒステリシス線は、強度 H の印加磁場の作用下で磁場の強度が増加するにつれて、磁性材料の磁気誘導が増加することを表します。
この磁気誘導は、磁気飽和に達した後は磁場の強さに追従しません。
磁気飽和に達すると、磁界強度の増加に従うことが困難になります。外部磁界の強さがゼロまでゆっくりと減少すると、減磁曲線はゼロ点を通過しても残留磁化 B を保持していることがわかります。
この残留磁化は、永久磁石の製造の一般原理、つまり、方向性のある磁化とそれに続く徐々に減磁することを示しています。逆磁場が印加されると、磁気誘導の強さはゼロになるか、逆方向に増加します。この超過分は保磁力 H と呼ばれます。
1.3 電磁力と機械エネルギー
モーターの最大の価値は、電気エネルギーを機械エネルギーに変換し、外部から仕事をして目的の動作を実行することです。
磁場中の荷電粒子の運動は、運動方向に垂直なローレンツ力の影響を受けます。その巨視的表現はアンペア力 Hm = Il * B であり、これは左手の法則を使用して判断できます。方向、
I は、磁場内の電流方向の導体の有効長です。
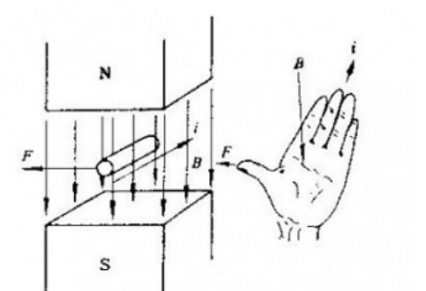
静電場 Fe=qE にも、対応する電場力が存在します。
そして、磁場と電場は両方ともそれ自体が場であり、その中の電荷または電流要素に加えられる力は体積と場の密度に依存するため、対応する場の力を場の観点から調べることができます。
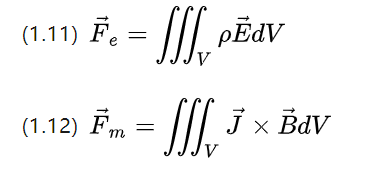
上記の 2 つの方程式はまだ対称性を維持しており、電界強度による特定の体積内の電荷密度 P は電気力密度 fe = pE を生成します。
磁界の強さに起因する特定の体積内の電流密度 J は、磁力密度 Fm = J * B を生成します (等方性材料および定電流の場合は、上式 (1.12) を使用する必要があります)。
この表現は、電磁場のエネルギーとエネルギー密度を直接調べることを私たちに促します。
このようにして、特定の点における電磁位置エネルギーは、対応する電磁力密度を取得するための勾配を見つけることによって決定され、調査対象の物体にかかる総電磁力を見つけることができます。
1.4 コイルモデル
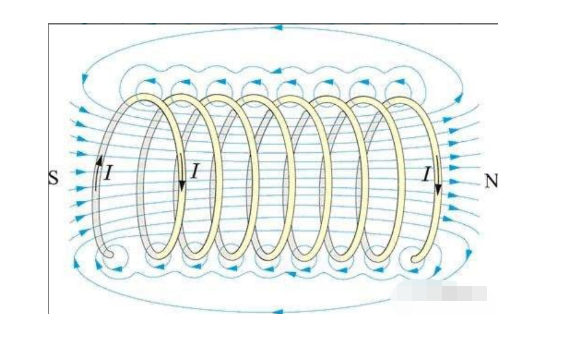
コイルは誘導電動機のモデルを形成する基本要素であり、AC 電動機の回路モデルと物体の物理モデルの橋渡しをします。
通電された導体の直線部分は、その周囲にトロイダル磁場を生成します (式 1.4 による)。
導体が最初と最後で閉じられると、トロイダル磁場によって導体リングの中心に磁力線が形成され、ソレノイドなどの導体リングを垂直に通過します。
通電された導体の電流のみを考慮すると、(1.4) は次のように単純化されます。
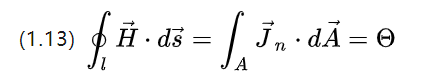
励磁場の強さの源である起磁力 (magnetische Durchfluchtung) は、基本的に [A] の閉じた導体のセクションを通過する合計電流の強さです。
実際には、通電されたワイヤはコイルに巻かれるため、ワイヤ電流は離散化され、(1.13) は次のように書き換えられます。
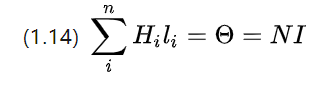
N はコイルの総巻き数、つまり巻き数です。
巻き数が多いほど総電流が大きくなり、磁気ポテンシャルが高くなり、より強い磁場を励起できることがわかります。
時間変化する磁場内の単一巻きコイルは、ワイヤの両端に電圧を誘導します。これは (1.3) で説明される現象です。
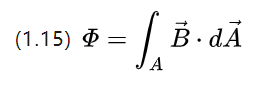
磁気誘導は、(1.3) を代入することで得られる磁束密度としても解釈できることがわかります。
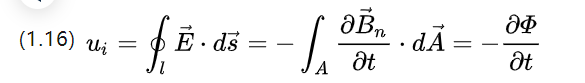
Ui は誘導電位であり、磁束変化の 2 つの形式を考えると、1 つはコイル面積を変更して磁束密度を変更するもので、次のとおりです。
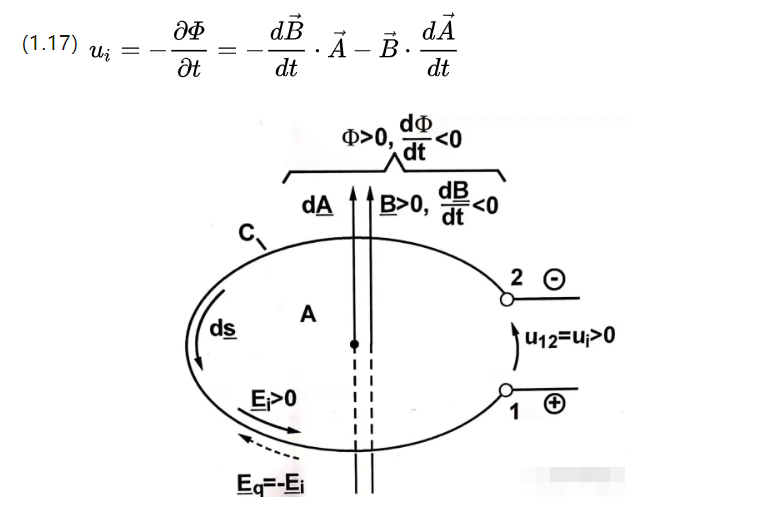
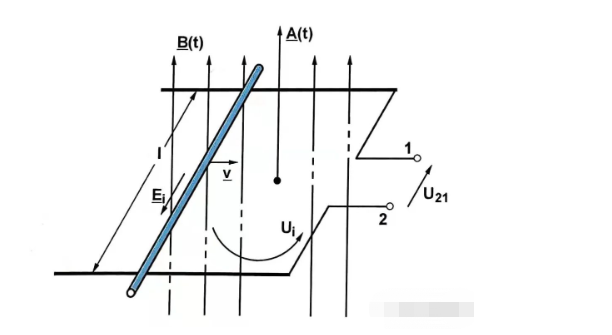
前者は形式的に変換された誘導電位(変換誘起電圧)であり、後者は並進変換された誘導電位(並進誘起電圧)である。
前者は磁束密度が時間変化するのに対し、後者は有効コイル面積が時間変化します。
この帰納原理は高校物理で言及されており、フルートの定理としても知られています。
コイルの巻き数が多い場合、有効磁束の合計は拡張されたコイルの巻き数の正確な整数倍になるため、磁気チェーンの概念が導入されます。
チェーンは次の図で定義されます。
磁気チェーンは、磁束と同様にスカラー量であることに注意してください。電流自体の変化も磁束の変化を引き起こす可能性があるため、磁束の変化が妨げられる傾向があります。これは次のように定義できます。
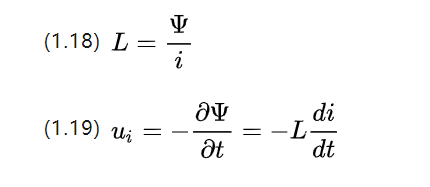
i は変化する電流の強さ、L はヘンリー [H] の自己インダクタンス係数で、そのサイズはコイルの体積の形状、巻き数、透磁率に関係します。
誘導電動機のコイルは、透磁率を高めるためにコイルの中央に鉄心などの強磁性体を入れ、鉄心にコイルを巻いているため、巻線と呼ばれています。
線形に均質な材料の部分の場合、その自己インダクタンス係数は次の式で近似できます。
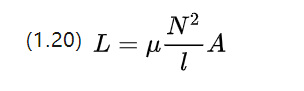
自己インダクタンスとは、コイル自体の電流が変化して抑制電圧現象を引き起こし、直流電動機の電流変化を妨げる傾向のことです。
2 つのコイルが互いに近づくと、それら自体の自己インダクタンスに加えて、隣接するコイルの電流も変化し、相互インダクタンスも発生します。
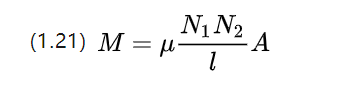
線形恒等性を持つ材料の相互インダクタンス係数は上の方程式で近似されます。この式は、相互インダクタンスが 2 つのコイルの同時巻き数の影響を受けることを示しています。
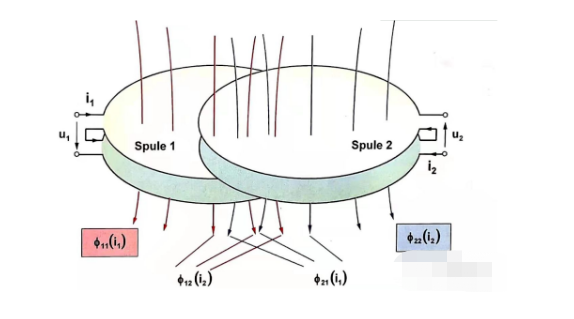
抵抗を無視し、隣接する 2 つのコイルの自己インダクタンスと相互インダクタンスを調べると、DC モータに関する電圧方程式を図 1.5 からリストできます。
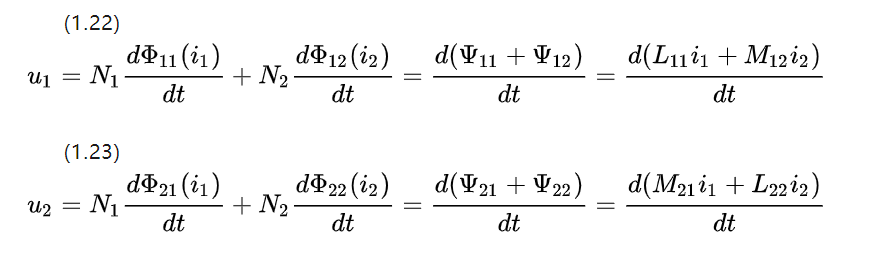
結合部分の材料パラメータと形状は同じであるため、結果として得られる相互インダクタンス係数は M12=M21 と等しくなります。
したがって、各コイルのカップリング チェーンのサイズは、DC モーターの対応するローター巻線コイルの電流強度に比例します。
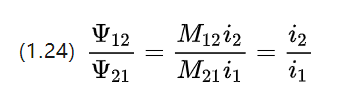
電気エネルギーと磁気回路に関する 1.5 オームの定理
中学校ではオームの定理を勉強しました。オームの定理では、導体の抵抗は両端の電圧と電流の比であり、抵抗材料自体を説明する公式があると述べています。
Q、これは導電率であり、正確に抵抗率 P の逆数であり、電流を流す能力を表します。
抵抗を適用することに加えて、電気モーターが動作するときの電圧と電流の関係は、導電率の図を使用して説明することもできます。
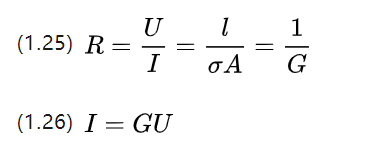
次に、単位面積あたりの電流強度、つまり電流密度 J = I/A e (e は単位ベクトル) を調べます。電流密度は、AC モーターの電流の方向を指すベクトルです。
これは、電圧方程式 U=E.l と組み合わせることができ、(1.25) は (1.26) を次のように書き換えることができます。
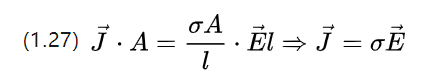
上の方程式は、顕微鏡レベルでのオームの定理、つまり導体に印加される一定の電界強度に対応する電流密度の変化を説明しています。
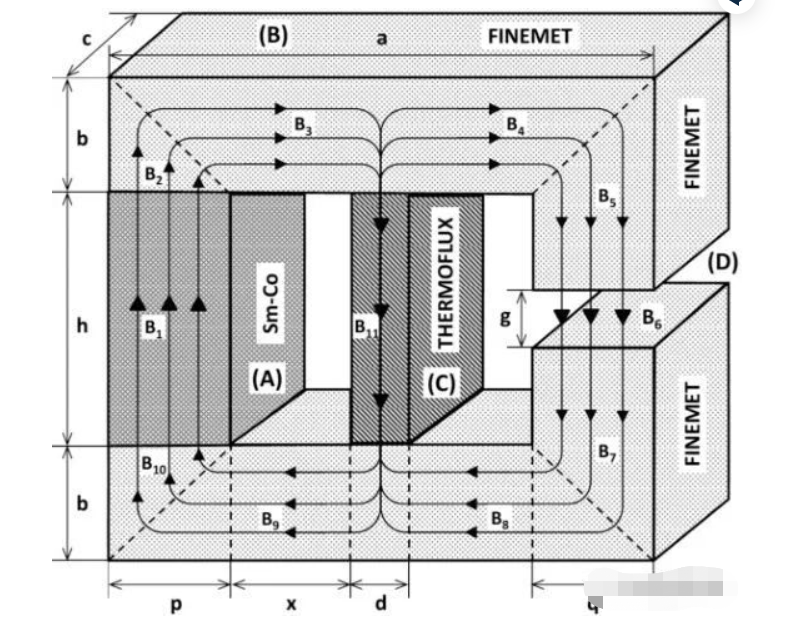
Lm は磁気回路のセクションを通る磁束の有効長で、A は対応する磁束面積です。
上の式は抵抗の式に非常に似ています。
磁気抵抗の式を再度変形してみましょう。引き続き次の値を得ることができます。
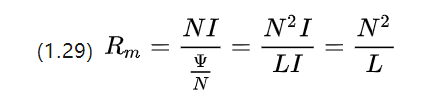
単位では、磁気抵抗は実際にはインダクタンス係数の逆数であることがわかります。
コンダクタンスの概念との類推を続けると、磁気コンダクタンス A (磁気ライトワート、[H] または [Ωs]) が得られます。
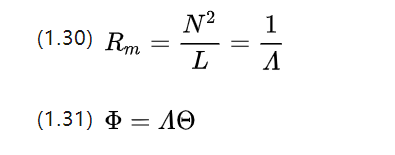
回路では、(1.26) の微分要素を求め、微視的なオームの定理が得られます。では、磁気回路に対応する微視的なオームの定理は何でしょうか?
磁束自体が磁束密度 B を持っていることに注意して、式 (1.31) を書き直すことができます。
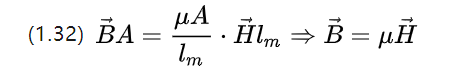
したがって、微視的な磁気回路のオームの定理は式 (1.10) であり、その下の磁界の強さは一定の磁界の磁化から得られる磁束密度です。
磁気抵抗の計算解析により、モータ巻線極、コア部、中間エアギャップ部全体の磁束の微小要素解析を実現することができ、離散有限要素解析FEM(Finite-Elemente-Methode)を実現できます。磁気回路全体のこと。
キルヒホッフの定理を磁気回路の回路に適用することもでき、非常に直感的で便利です。
電気モーターに関する詳しい情報をコメント欄で共有していただければ幸いです。
電動モーターに関するご質問は、電動モーターの専門家にお問い合わせください。 メーカー で 中国 次のように:

東春モーターは、輸送、インフラ、建設などのさまざまな産業で使用される幅広い電動モーターを取り揃えています。
すぐに返信してください。








