יסודות פיזיים של מנועים חשמליים

1. העיקרון הפיזי של עבודת מנוע חשמלי

1.1 מערכת המשוואות של מקסוול

המנוע החשמלי הוא מתמר הממיר כל הזמן אנרגיה אלקטרומגנטית ואנרגיה מכנית.

כאשר אנרגיה חשמלית מוזנת, המנוע החשמלי יכול להפיק מומנט ואנרגיה מכנית באופן רציף.

כלומר, המנוע החשמלי; לעומת זאת, אם כוח חיצוני דוחף ברציפות את פיר המנוע החשמלי ומכניס אנרגיה מכנית, המנוע החשמלי יכול להפיק באופן רציף מתח ואנרגיה חשמלית מקצה החוט בהיפוך, כלומר, הגנרטור.

מבחינה היסטורית, השנאי הסטטי נספר גם כמנוע חשמלי, אך הוא התפתח בהדרגה והתייחס אך ורק למנועים חשמליים ולגנרטורים.

אחד היתרונות של מנועים חשמליים הוא שההפסדים שלהם קטנים יחסית, ולכן הם משיגים יעילות גבוהה.

מנועים חשמליים גדולים יכולים להשיג יעילות של עד 99%.

כשמדברים על מערכות אלקטרומגנטיות, מערכת המשוואות של מקסוול היא בלתי נמנעת.

בעולם המקרוסקופי ואפילו בעולם המיקרוסקופי,

ניתן להשתמש במערכת המשוואות של מקסוול ביעילות רבה לתיאור מאפייני המערכת.

מערכת המשוואות של מקסוול סוכמה ממחקרים קודמים על תופעות אלקטרומגנטיות.

ישנן ארבע משוואות בסיסיות מאוד, הן בצורה דיפרנציאלית והן בצורה אינטגרלית.

כעת נבחן את מערכת המשוואות של מקסוול בצורה אינטגרלית.

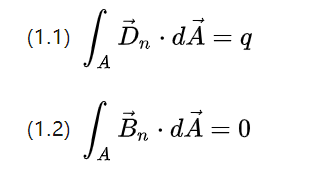
שתי המשוואות לעיל מתארות את השטף של צפיפות השדה, בהתאמה, את סך תמונת ההזזה של פוטנציאל היציאה ואת סך תמונת השראת השדה המגנטי המסתובב במשטח חלל סגור

על פי הידע שנלמד בתיכון, השדה החשמלי יכול להיווצר על ידי עירור מטען נקודתי, את השדה המגנטי לא ניתן לעורר על ידי המונופול המגנטי, אלא כדי להאריך את הנתיב הסגור, כך שהשדה החשמלי פעיל, השדה המגנטי הוא פַּסִיבִי.

אז שטף ההזזה הפוטנציאלי הכולל הוא סך המטען q והשטף המגנטי הכולל הוא 0.

שתי המשוואות לעיל מתארות את כמויות הספין של עוצמת השדה, האינטגרלים של עוצמת השדה החשמלי הכוללת ועוצמת השדה המגנטי הכוללת.

בהתאמה לקצב השינוי של השטף המגנטי וקצב השינוי של הסטת הפוטנציאל (עוצמת הזרם), בהתאמה, לפנייה אחת לאורך מסלול העקומה בעקומת חלל סגור.

נוסחאות גאוס וסטוקס מאפשרות גם את השכתוב של ארבע המשוואות לעיל לצורה דיפרנציאלית כדלקמן.

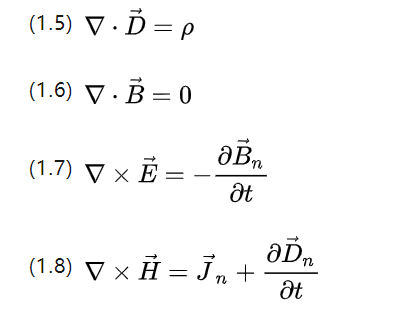
▽ עבור האופרטור Nabla, עם מכפלת נקודות וקטור לחישוב מכפלת הפיזור ומזלג לחישוב הספין, P עבור צפיפות גוף המטען, ו-Jn עבור צפיפות הנוכחית.

המשוואות לעיל יכולות לתאר בעצם את כל ההתנהגות האלקטרומגנטית המתרחשת בכל מערכות מנועי אינדוקציה AC

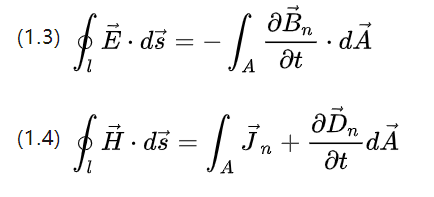
1.2 קיטוב חומרים ומגנטיזציה לאנרגיה חשמלית

בשדה מגנטי מסתובב חשמלי מופעל, מולקולות החומר ישנו את הכיוון שלהן מכיוון שהקוטביות מושפעת מעוצמת השדה.

התחומים החשמליים שנוצרו על ידי הקבוצות המולקולריות המקוריות המסודרות באופן לא אחיד בגדלים שונים יהיו מקוטבים בגלל השדה המגנטי המופעל, וכיוון חלוקת המטען מתכנס.

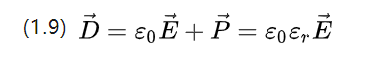
E0=8.854187817*10-12F/m היא הפרמיטיביות של הוואקום, שהיא גם הקבוע הדיאלקטרי של הוואקום, ו-P הוא הקבוע הדיאלקטרי היחסי, שנקבע על ידי תכונות החומר עצמו.

(1.9) מתאר את צפיפות ההסטה הפוטנציאלית של השדה החשמלי המופעל ותמונת עוצמת הקיטוב המתאימה יחד.

בשדה מגנטי מיושם, ניתן להשיג את התחומים המגנטיים המתאימים ואת עוצמות המגנטיזציה באותו אופן.

בניגוד לשדה החשמלי, מוכנס חוזק קיטוב מגנטי M, המתאר את ההבדל בין חוזק האינדוקציה המגנטית של החומר לזה של סביבת הוואקום.

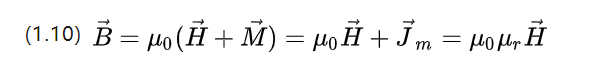
U0=4π*10-7 N.A-2 היא חדירות הוואקום ו-Ur היא החדירות היחסית, המתארת ​​את יכולת החומר לאפשר לשדה מגנטי לעבור דרכו.

אם Ur<=1 הוא אנטי מגנטי, החומר מונע מעבר של שדה מגנטי; אם התמונה פרמגנטית, החומר תואם למעבר של שדה מגנטי.

אם Ur>=1o 5 הוא פרומגנטי, החומר כגון ניקל בר-קובלט ישפר את השדה המגנטי לאחר המגנטיזציה. ואז לשמור על חוזק מסוים של שדה מגנטי לאחר הסרת השדה המגנטי, אשר נקרא מגנטיות רמננטית.

בתהליך פעולת המנוע תהיה מגנטיזציה ודה-מגנטיזציה מתמדת, ולכן יש לשים לב גם לבדיקת קווי ההיסטרזיס של חומרים שונים.

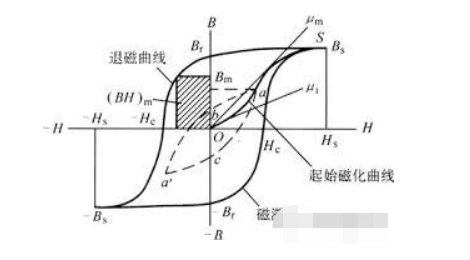
קו ההיסטרזיס מתאר את ההשראה המגנטית ההולכת וגוברת של חומר מגנטי ככל שעוצמת השדה גדלה תחת פעולת שדה מגנטי מופעל בעוצמה H.

אינדוקציה מגנטית זו אינה עוקבת אחר עוצמת השדה לאחר הגעה לרוויה מגנטית.

לאחר הגעה לרוויה המגנטית, קשה לעקוב אחר העלייה בעוצמת השדה. כאשר עוצמת השדה המגנטי החיצוני פוחתת לאט לאפס, ניתן לראות שעקומת הדה-מגנטיזציה עדיין שומרת על המגנטיזציה הרמננטית B כאשר היא עוברת את נקודת האפס.

מגנטיזציה רמננטית זו מציגה את העיקרון הכללי של ייצור מגנטים קבועים, כלומר, מגנטיזציה כיוונית ואחריה דה-מגנטיזציה הדרגתית. כאשר השדה המגנטי ההפוך מופעל, עוצמת האינדוקציה המגנטית מגיעה לאפס או אפילו עולה בכיוון ההפוך, והעודף הזה נקרא הכפייה H.

1.3 כוח אלקטרומגנטי ואנרגיה מכנית

הערך הגדול ביותר של המנוע הוא לממש את ההמרה של אנרגיה חשמלית לאנרגיה מכנית, לבצע עבודה חיצונית ולבצע את תנועת המטרה.

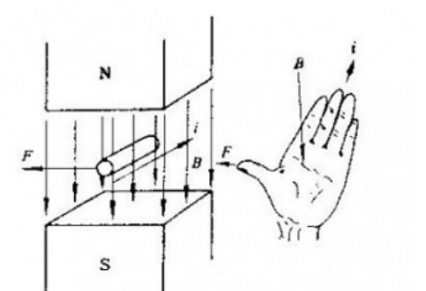
תנועתו של חלקיק טעון בשדה מגנטי כפופה לכוח לורנץ בניצב לכיוון התנועה, שביטויו המקרוסקופי הוא כוח אמפר Hm = Il * B , אותו ניתן לשפוט באמצעות כלל יד שמאל לקביעת כיוון,

I הוא האורך האפקטיבי של המוליך בשדה המגנטי בכיוון הזרם.

יש גם כוח שדה חשמלי מתאים בשדה האלקטרוסטטי Fe=qE .

וגם שדות מגנטיים וחשמליים הם בעצמם שדות, והכוח המופעל על יסוד המטען או הזרם שבהם תלוי בנפח ובצפיפות השדה, וכך ניתן לבחון את כוח השדה המקביל במונחים של השדה.

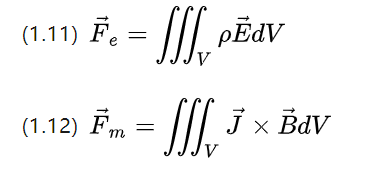
שתי המשוואות לעיל עדיין שומרות על הסימטריה, צפיפות המטען P בנפח מסוים עקב עוצמת השדה של השדה החשמלי מייצרת את צפיפות הכוח החשמלי fe = pE,

צפיפות הזרם J בנפח מסוים עקב עוצמת השדה המגנטי מייצרת את צפיפות הכוח המגנטי Fm = J * B (יש להשתמש במשוואה לעיל (1.12) במקרה של חומרים איזוטריים וזרם קבוע).

ביטוי זה נותן לנו השראה לבחון ישירות את האנרגיה וצפיפות האנרגיה של השדה האלקטרומגנטי.

בדרך זו, ניתן לקבוע את האנרגיה הפוטנציאלית האלקטרומגנטית בנקודה מסוימת על ידי מציאת השיפוע כדי לקבל את צפיפות הכוח האלקטרומגנטי המתאימה ובכך למצוא את הכוח האלקטרומגנטי הכולל על העצם הנחקר.

דגם 1.4 סליל

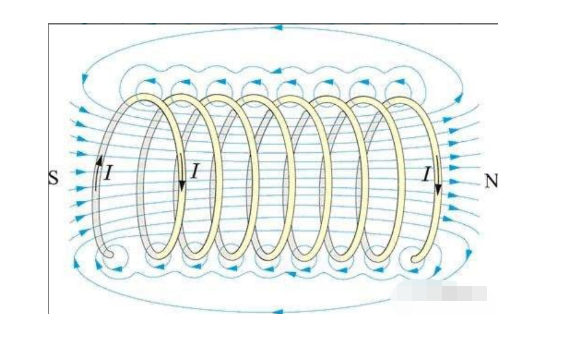
סליל הוא אלמנט בסיסי שיוצר מודל של מנועי אינדוקציה, המגשר בין דגם המעגל של מנוע ה-AC והמודל הפיזי של האובייקט.

קטע ישר של מוליך מופעל יוצר סביבו שדה מגנטי טורואידי (לפי משוואה 1.4).

כאשר המוליך סגור בהתחלה ובסוף, השדה הטורואידי יוצר קווי כוח מגנטיים במרכז טבעת המוליך העוברים אנכית דרך טבעת המוליך, כמו סולנואיד.

בהתחשב רק בזרם המוליך המופעל, (1.4) מפשט ל:

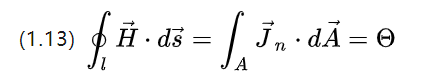
הכוח המגנטו-מוטיבי (magnetische Durchfluchtung), שהוא המקור לחוזק של שדה העירור, הוא בעצם עוצמתו של הזרם הכולל העובר דרך קטע של מוליך סגור ב-[A].

מכיוון שבפועל החוט המופעל יתפתל לסליל, זרם החוט עובר דיסקרטיות ו-(1.13) נכתב מחדש כ

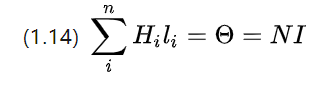
N הוא המספר הכולל של פיתולים בסליל, כלומר, מספר הסיבובים.

ניתן לראות שאם מספר הסיבובים גבוה יותר, הזרם הכולל גבוה יותר, הפוטנציאל המגנטי גבוה יותר, וככל שניתן לעורר את השדה המגנטי חזק יותר.

סליל בסיבוב בודד בשדה מגנטי משתנה בזמן יגרום למתח בשני קצוות החוט, תופעה המתוארת על ידי (1.3).

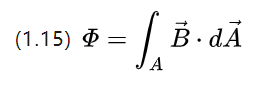
ניתן להבין שניתן לפרש את האינדוקציה המגנטית גם כצפיפות השטף המגנטי, שניתן להשיג על ידי החלפה (1.3)

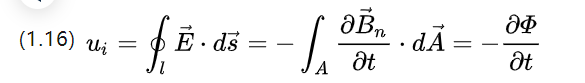
Ui הוא הפוטנציאל החשמלי המושרה, שקול שתי צורות של שינוי שטף, האחת היא לשנות את אזור הסליל אך לשנות את צפיפות השטף, ואז יש כדלקמן;

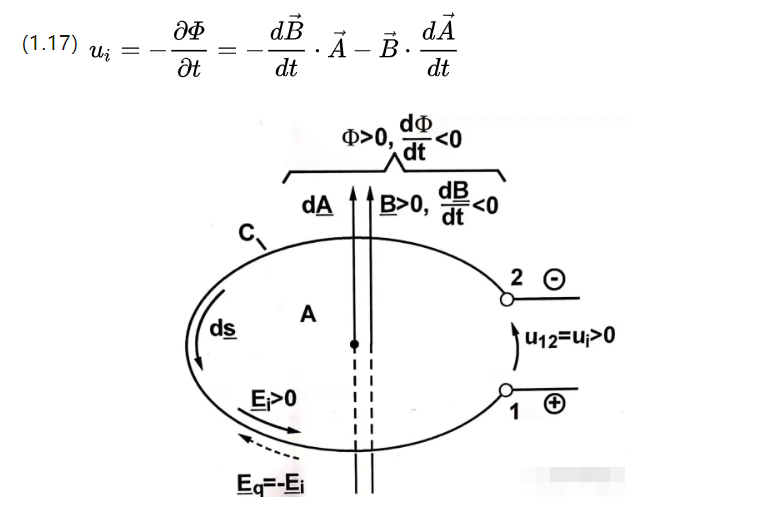
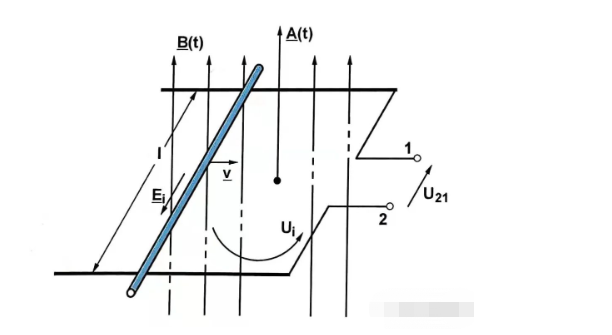
החלק הראשון הוא פוטנציאל האינדוקציה שעבר טרנספורמציה (מתח המושרה בטרנספורמציה) והחלק השני הוא פוטנציאל האינדוקציה שעבר טרנספורמציה (מתח המושרה בטרנספורמציה).

לראשון יש צפיפות שטף מגנטי המשתנה בזמן, בעוד שלאחרון יש אזור סליל יעיל משתנה בזמן.

עקרון האינדוקציה הזה מוזכר בפיזיקה של תיכון וידוע גם כמשפט החליל.

כאשר לסליל יש סיבובים רבים, השטף האפקטיבי הכולל הוא בדיוק כפולה שלמה של סיבובי הסליל המורחבים, ובכך מציגים את המושג של שרשרת מגנטית.

השרשרת מוגדרת באיור למטה.

שימו לב שהשרשרת המגנטית היא כמות סקלרית, בדיוק כמו השטף המגנטי. מכיוון ששינוי בזרם עצמו יכול גם לגרום לשינוי בשטף, הנטייה היא לעכב את שינוי השטף, שניתן להגדיר כך:

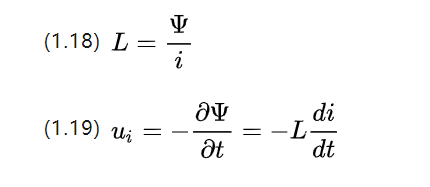
i הוא עוצמת הזרם המשתנה, L הוא מקדם ההשראות העצמית בהנרי [H], וגודלו קשור לצורת נפח הסליל, מספר הסיבובים והחדירות המגנטית.

סלילים במנועי אינדוקציה עשויים להיות בעלי חומר פרומגנטי באמצע הסליל, כמו ליבת ברזל, על מנת להגביר את החדירות המגנטית, כך שהסליל מתלכד על ליבת הברזל, ומכאן השם פיתול.

עבור קטע של חומר הומוגני ליניארי, ניתן להעריך את מקדם ההשראות העצמית שלו באמצעות המשוואה הבאה

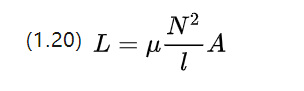
השראות עצמית היא סליל של שינויים בזרם משלו כדי לגרום לתופעה של מתח דיכוי, נטייתו לעכב שינויי זרם לגבי מנוע חשמלי DC.

כאשר שני סלילים קרובים זה לזה, בנוסף להשראות העצמית שלהם, אלא גם בגלל הסלילים השכנים על השינויים הנוכחיים והשראות הדדית

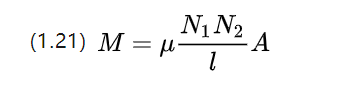
מקדם ההשראות ההדדית של חומרים בעלי זהויות ליניאריות משוער על ידי המשוואה לעיל, המראה שההשראות ההדדית מושפעת ממספר הסיבובים של שני הסלילים בו זמנית.

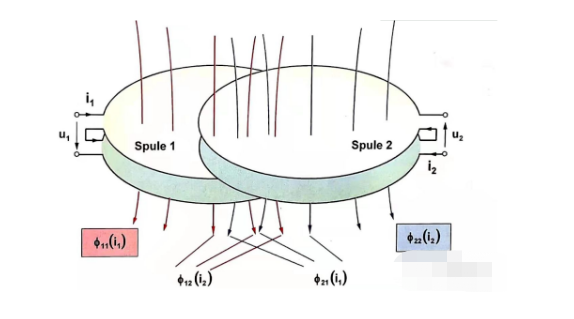
בהתעלמות מההתנגדות ובחינת ההשראות העצמית וההדדית של שני הסלילים הסמוכים, ניתן לרשום את משוואת המתח מאיור 1.5 לגבי מנועי DC

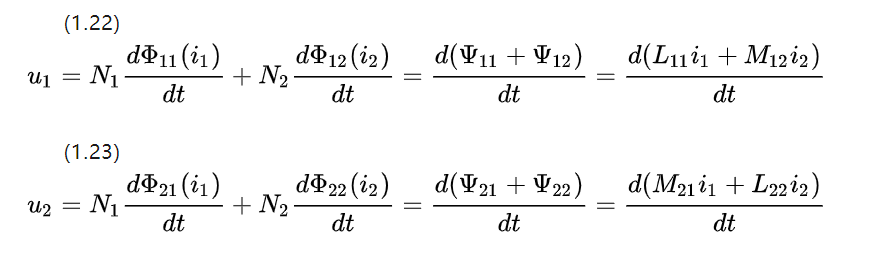
מכיוון שלחלקי הצימוד יש אותם פרמטרים וצורת חומר, מקדמי השראות ההדדיים המתקבלים שווים M12=M21.

אז הגודל של שרשראות הצימוד על כל סליל הוא פרופורציונלי לחוזק הזרם על סליל פיתולי הרוטור המקביל עבור מנוע DC.

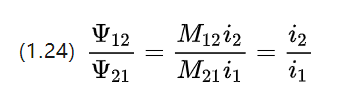
משפט 1.5 אוהם לאנרגיה חשמלית ומעגלים מגנטיים

בבית הספר התיכון למדנו את משפט אוהם, הקובע שהתנגדות של מוליך היא היחס בין המתח והזרם בשני הקצוות, ושיש נוסחה לתיאור החומר ההתנגדות עצמו.

Q, שהיא המוליכות, שהיא בדיוק ההדדיות של ההתנגדות P ומתארת ​​את היכולת להוביל זרם.

בנוסף להפעלת התנגדות, ניתן לתאר את הקשר בין מתח לזרם באמצעות תמונת המוליכות כאשר המנוע החשמלי פועל.

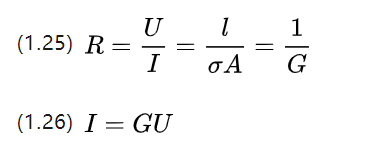
כעת בחנו את עוצמת הזרם ליחידת שטח, כלומר, צפיפות הזרם J = I/A e (e הוא וקטור היחידה), כאשר צפיפות הזרם כווקטור מצביע לכיוון הזרם עבור מנועי AC.

ניתן לשלב זאת עם משוואת המתח U=E.l ו-(1.25) לשכתב (1.26) כ

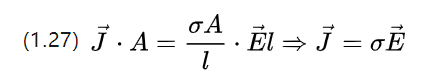
המשוואה שלעיל מתארת ​​את משפט אוהם ברמה המיקרוסקופית, כלומר את השונות של צפיפות הזרם התואמת לחוזק שדה קבוע המופעל על המוליך.

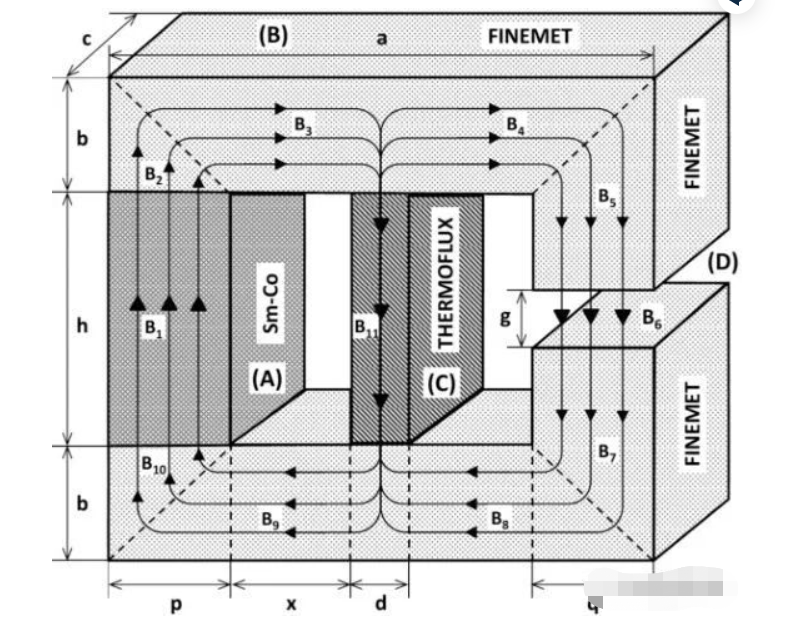
Lm הוא האורך האפקטיבי של השטף המגנטי דרך קטע של המעגל המגנטי, ו-A הוא אזור השטף המתאים.

המשוואה שלעיל דומה מאוד לנוסחת ההתנגדות.

תנו לנו לעוות שוב את נוסחת ההתנגדות למגנט ונוכל להמשיך להשיג

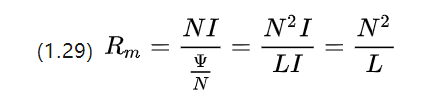
ניתן לראות שביחידות ההתנגדות המגנטורית היא למעשה היפוך של מקדם השראות.

בהמשך האנלוגיה למושג המוליכות, נקבל את המוליכות המגנטית A (מגנטית Leitwert, ב-[H] או [Ωs])

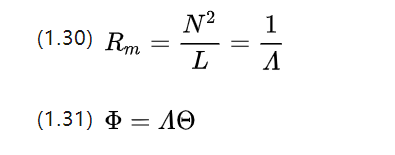
במעגל נמצא את האלמנטים הדיפרנציאליים עבור (1.26) ומקבלים את משפט אוהם המיקרוסקופי, אז מהו משפט אוהם המיקרוסקופי המקביל למעגל המגנטי?

אנו יכולים להמשיך לשכתב את המשוואה (1.31), ולציין שלשטף המגנטי עצמו יש צפיפות שטף B, אשר לאחר מכן מניבה

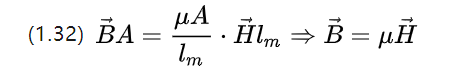
אז משפט המעגל המגנטי המיקרוסקופי של אוהם הוא משוואה (1.10), ועוצמת השדה המגנטי מתחת היא צפיפות השטף המתקבלת ממגנטיזציה של שדה מגנטי קבוע.

ניתן להשתמש בניתוח החישובי של הרתיעה כדי לממש ניתוח מיקרו-אלמנטים של השטף בכל עמוד מתפתל המנוע, חלק הליבה וחלק מרווח אוויר ביניים, אשר יכול לממש ניתוח אלמנט סופי בדיד FEM (Finite-Elemente-Methode) של כל המעגל המגנטי.

אפשר גם ליישם את משפט קירכהוף למעגל במעגל המגנטי, שהוא מאוד אינטואיטיבי ונוח.

מוזמנים לשתף אותנו במידע נוסף על מנועים חשמליים באזור ההערות!

כל שאלה לגבי מנוע חשמלי, אנא פנה אל המנוע החשמלי המקצועי יַצרָן ב חרסינה כדלהלן:

למנוע דונגצ'ון מגוון רחב של מנועים חשמליים המשמשים בתעשיות שונות כגון תחבורה, תשתיות ובנייה.

קבל תשובה מהירה.