1. Das physikalische Prinzip der Arbeit eines Elektromotors
1.1 Maxwells Gleichungssystem
Der Elektromotor ist ein Wandler, der ständig elektromagnetische Energie und mechanische Energie umwandelt.
Bei Eingabe elektrischer Energie kann der Elektromotor kontinuierlich Drehmoment und mechanische Energie abgeben.
d. h. der Elektromotor; Wenn umgekehrt eine äußere Kraft die Welle des Elektromotors kontinuierlich drückt und mechanische Energie einspeist, kann der Elektromotor im umgekehrten Fall kontinuierlich Spannung und elektrische Energie vom Drahtende, d. h. dem Generator, abgeben.
Historisch gesehen wurde der statische Transformator auch zu den Elektromotoren gezählt, doch nach und nach entwickelte sich dieser Begriff dahingehend, dass er sich ausschließlich auf Elektromotoren und Generatoren bezog.
Einer der Vorteile von Elektromotoren besteht darin, dass ihre Verluste relativ gering sind und sie daher einen hohen Wirkungsgrad erreichen.
Große Elektromotoren können Wirkungsgrade von bis zu 99 % erreichen.

Wenn man über elektromagnetische Systeme spricht, ist das Maxwellsche Gleichungssystem unvermeidlich.
In der makroskopischen Welt und sogar in der mikroskopischen Welt,
Das Maxwellsche Gleichungssystem kann sehr effektiv zur Beschreibung der Systemeigenschaften eingesetzt werden.
Maxwells Gleichungssystem wurde aus früheren Studien elektromagnetischer Phänomene zusammengefasst.
Es gibt vier sehr grundlegende Gleichungen, sowohl in Differential- als auch in Integralform.
Betrachten wir nun Maxwells Gleichungssystem in Integralform.
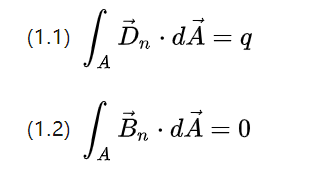
Die beiden obigen Gleichungen beschreiben den Fluss der Felddichte bzw. die Summe des Abflusspotentialverschiebungsbildes und die Summe des rotierenden Magnetfeldinduktionsbildes in einer geschlossenen Raumoberfläche
Nach dem in der High School erlernten Wissen kann das elektrische Feld durch Punktladungsanregung erzeugt werden, das magnetische Feld kann nicht durch den magnetischen Monopol angeregt werden, sondern um den Pfad zu verlängern, der geschlossen ist, sodass das elektrische Feld aktiv ist, ist das magnetische Feld aktiv passiv.
Der gesamte Potentialverschiebungsfluss ist also die Gesamtladung q und der gesamte magnetische Fluss ist 0.
Die beiden obigen Gleichungen beschreiben die Spingrößen der Feldstärke, die Integrale der gesamten elektrischen Feldstärke und der gesamten magnetischen Feldstärke.
Entspricht der Änderungsrate des magnetischen Flusses bzw. der Änderungsrate der Potentialverschiebung (Stromstärke) für eine Umdrehung entlang des Kurvenverlaufs auf einer Kurve im geschlossenen Raum.
Die Gauß- und Stokes-Formeln ermöglichen auch die Umschreibung der oben genannten vier Gleichungen in Differentialform wie folgt.
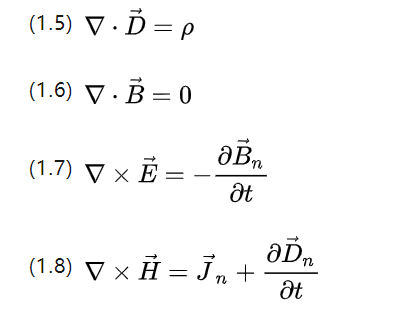
▽ für den Nabla-Operator, mit Vektorskalarprodukt zur Berechnung der Streuung und Gabelprodukt zur Berechnung des Spins, P für die Ladungskörperdichte und Jn für die Stromdichte.
Die obigen Gleichungen können grundsätzlich das gesamte elektromagnetische Verhalten beschreiben, das in allen Wechselstrom-Induktionsmotorsystemen auftritt
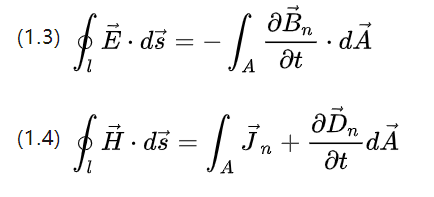
1.2 Materialpolarisierung und Magnetisierung für elektrische Energie
In einem angelegten elektrischen rotierenden Magnetfeld ändern die Materialmoleküle ihre Ausrichtung, da die Polarität von der Feldstärke beeinflusst wird.
Die durch die ursprünglich ungleichmäßig angeordneten Molekülgruppen unterschiedlicher Größe gebildeten elektrischen Domänen werden aufgrund des angelegten Magnetfelds polarisiert und die Ausrichtung der Ladungsverteilung konvergiert.
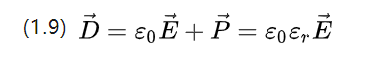
E0=8,854187817*10-12F/m ist die Vakuumpermittivität, die auch die Vakuumdielektrizitätskonstante ist, und P ist die relative Dielektrizitätskonstante, die durch die Eigenschaften des Materials selbst bestimmt wird.
(1.9) beschreibt die Potentialverschiebungsdichte des angelegten elektrischen Feldes und das entsprechende Polarisationsintensitätsbild zusammen.
In einem angelegten Magnetfeld können auf die gleiche Weise die entsprechenden magnetischen Domänen und Magnetisierungsstärken erhalten werden.
Im Gegensatz zum elektrischen Feld wird eine magnetische Polarisationsstärke M eingeführt, die den Unterschied zwischen der magnetischen Induktionsstärke des Materials und der der Vakuumumgebung beschreibt.
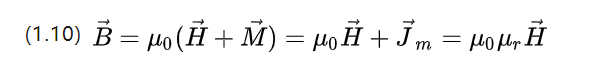
U0=4π*10-7 N.A-2 ist die Vakuumpermeabilität und Ur ist die relative Permeabilität, die die Fähigkeit des Materials beschreibt, ein Magnetfeld durchzulassen.
Wenn Ur<=1 ist antimagnetisch, das Material verhindert den Durchgang eines Magnetfeldes; Wenn das Bild paramagnetisch ist, unterliegt das Material dem Durchgang eines Magnetfelds.
Wenn Ur>=1o 5 ist ferromagnetisch, das Material wie Ferro-Kobalt-Nickel verstärkt das Magnetfeld nach der Magnetisierung. Und dann behalten sie nach dem Entfernen des Magnetfelds eine bestimmte Stärke des Magnetfelds bei, was als remanenter Magnetismus bezeichnet wird.
Während des Motorbetriebs kommt es zu einer ständigen Magnetisierung und Entmagnetisierung, daher sollte auch auf die Untersuchung der Hystereselinien verschiedener Materialien geachtet werden.
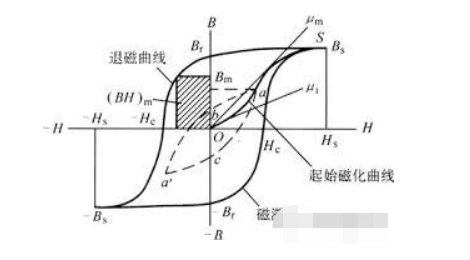
Die Hystereselinie beschreibt die zunehmende magnetische Induktion eines magnetischen Materials mit zunehmender Feldstärke unter Einwirkung eines angelegten Magnetfelds der Stärke H.
Diese magnetische Induktion folgt nach Erreichen der magnetischen Sättigung nicht mehr der Feldstärke.
Nach Erreichen der magnetischen Sättigung ist es schwierig, den Anstieg der Feldstärke zu verfolgen. Wenn die äußere Magnetfeldstärke langsam auf Null absinkt, erkennt man, dass die Entmagnetisierungskurve beim Passieren des Nullpunkts immer noch die remanente Magnetisierung B beibehält.
Diese remanente Magnetisierung zeigt das allgemeine Prinzip der Herstellung von Permanentmagneten, d. h. eine gerichtete Magnetisierung gefolgt von einer allmählichen Entmagnetisierung. Wenn das umgekehrte Magnetfeld angelegt wird, geht die magnetische Induktionsstärke auf Null oder nimmt sogar in die entgegengesetzte Richtung zu, und dieser Überschuss wird Koerzitivfeldstärke H genannt.
1.3 Elektromagnetische Kraft und mechanische Energie
Der größte Nutzen des Motors besteht darin, die Umwandlung von elektrischer Energie in mechanische Energie zu realisieren, Arbeit von außen zu verrichten und die Zielbewegung auszuführen.
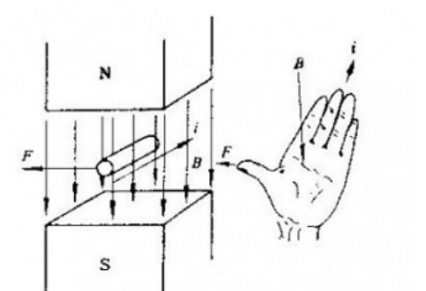
Die Bewegung eines geladenen Teilchens in einem Magnetfeld unterliegt der Lorentz-Kraft senkrecht zur Bewegungsrichtung, deren makroskopischer Ausdruck die Ampere-Kraft Hm = Il * B ist, die mithilfe der Linke-Hand-Regel zur Bestimmung der beurteilt werden kann Richtung,
I ist die effektive Länge des Leiters im Magnetfeld in Stromrichtung.
Es gibt auch eine entsprechende elektrische Feldkraft im elektrostatischen Feld Fe=qE .
Und sowohl magnetische als auch elektrische Felder sind selbst Felder, und die auf die Ladung oder das Stromelement in ihnen ausgeübte Kraft hängt vom Volumen und der Felddichte ab, und daher kann die entsprechende Feldkraft anhand des Feldes untersucht werden.
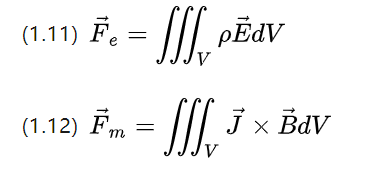
Die beiden obigen Gleichungen behalten immer noch die Symmetrie bei, die Ladungsdichte P in einem bestimmten Volumen erzeugt aufgrund der Feldstärke des elektrischen Feldes die elektrische Kraftdichte fe = pE,
Die Stromdichte J in einem bestimmten Volumen aufgrund der magnetischen Feldstärke ergibt die magnetische Kraftdichte Fm = J * B (bei isotropen Materialien und konstantem Strom muss die obige Gleichung (1.12) verwendet werden).
Dieser Ausdruck inspiriert uns, die Energie und Energiedichte des elektromagnetischen Feldes direkt zu untersuchen.
Auf diese Weise kann die elektromagnetische potentielle Energie an einem bestimmten Punkt bestimmt werden, indem der Gradient ermittelt wird, um die entsprechende elektromagnetische Kraftdichte zu erhalten und so die gesamte elektromagnetische Kraft auf das untersuchte Objekt zu ermitteln.
1.4 Spulenmodell
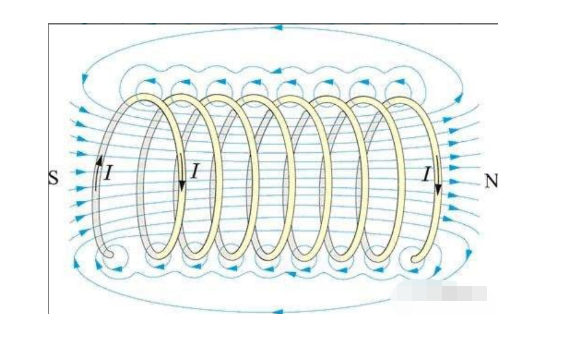
Eine Spule ist ein grundlegendes Element, das ein Modell von Induktionsmotoren bildet und eine Brücke zwischen dem Schaltungsmodell des Wechselstrommotors und dem physikalischen Modell des Objekts bildet.
Ein gerader Abschnitt eines unter Spannung stehenden Leiters erzeugt um ihn herum ein torusförmiges Magnetfeld (gemäß Gleichung 1.4).
Wenn der Leiter am Anfang und Ende geschlossen ist, bildet das Ringfeld magnetische Kraftlinien in der Mitte des Leiterrings, die vertikal durch den Leiterring verlaufen, wie z. B. eine Magnetspule.
Betrachtet man nur den Strom auf dem unter Spannung stehenden Leiter, vereinfacht sich (1.4) zu:
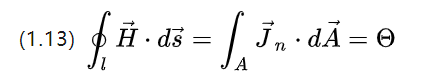
Die magnetomotorische Kraft (magnetische Durchfluchtung), die die Quelle der Stärke des Erregerfeldes ist, ist im Wesentlichen die Stärke des Gesamtstroms, der durch einen Abschnitt eines geschlossenen Leiters fließt, in [A].
Da in der Praxis der unter Spannung stehende Draht zu einer Spule gewickelt wird, wird der Drahtstrom diskretisiert und (1.13) umgeschrieben als
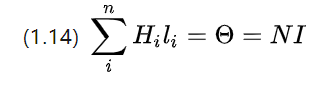
N ist die Gesamtzahl der Windungen in der Spule, also die Anzahl der Windungen.
Man erkennt, dass je höher die Windungszahl, desto höher der Gesamtstrom, desto höher das magnetische Potential und desto stärker kann das Magnetfeld angeregt werden.
Eine Spule mit einer Windung in einem zeitlich veränderlichen Magnetfeld induziert an beiden Enden des Drahtes eine Spannung, ein Phänomen, das durch (1.3) beschrieben wird.
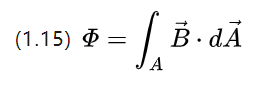
Es versteht sich, dass die magnetische Induktion auch als magnetische Flussdichte interpretiert werden kann, die durch Einsetzen von (1.3) erhalten werden kann
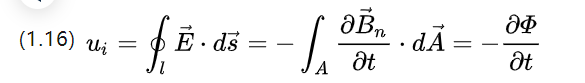
Ui ist das induzierte elektrische Potential. Betrachten Sie zwei Formen der Flussänderung: Eine besteht darin, die Spulenfläche zu ändern, aber die Flussdichte zu ändern. Dann gibt es Folgendes:
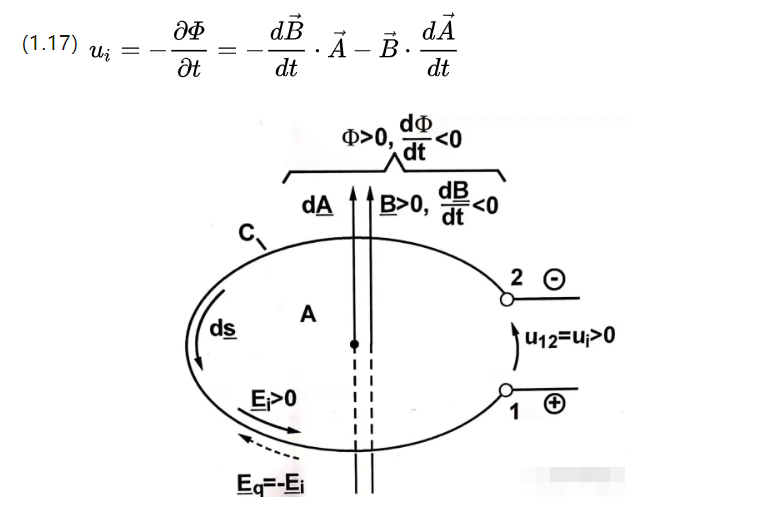
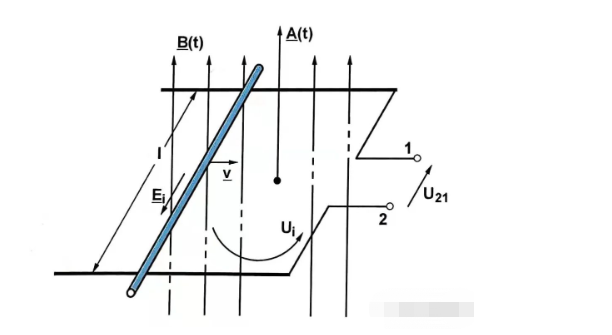
The former part is the formally transformed induction potential (transformatisch induzierte Spannung) and the latter part is the translationally transformed induction potential (translatorisch induzierte Spannung).
Ersteres weist eine zeitlich veränderliche magnetische Flussdichte auf, während letzteres eine zeitlich veränderliche effektive Spulenfläche aufweist.
Dieses Induktionsprinzip wird in der Oberstufenphysik erwähnt und ist auch als Flötensatz bekannt.
Wenn eine Spule viele Windungen hat, ist der gesamte effektive Fluss genau ein ganzzahliges Vielfaches der ausgedehnten Spulenwindungen, womit das Konzept einer magnetischen Kette eingeführt wird.
Die Kette ist in der folgenden Abbildung definiert.
Beachten Sie, dass die magnetische Kette genau wie der magnetische Fluss eine skalare Größe ist. Da eine Änderung des Stroms selbst auch eine Änderung des Flusses verursachen kann, besteht die Tendenz darin, die Änderung des Flusses zu behindern, was wie folgt definiert werden kann:
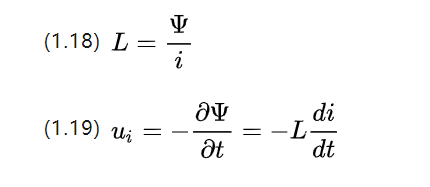
i ist die variierende Stromstärke, L ist der Selbstinduktivitätskoeffizient in Henry [H] und seine Größe hängt von der Form des Spulenvolumens, der Anzahl der Windungen und der magnetischen Permeabilität ab.
Spulen in Induktionsmotoren bestehen aus ferromagnetischem Material in der Mitte der Spule, beispielsweise einem Eisenkern, um die magnetische Permeabilität zu erhöhen, sodass die Spule auf den Eisenkern gewickelt ist, daher der Name Wicklung.
Für einen Abschnitt aus linear homogenem Material kann sein Selbstinduktivitätskoeffizient durch die folgende Gleichung angenähert werden
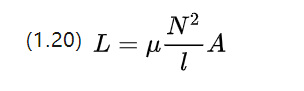
Bei der Selbstinduktivität handelt es sich um eine Spule, die ihren eigenen Strom ändert, um das Phänomen der Unterdrückungsspannung zu induzieren, d. h. ihre Tendenz, Stromänderungen bei Gleichstrommotoren zu behindern.
Wenn zwei Spulen nahe beieinander liegen, kommt es neben der eigenen Selbstinduktivität auch zu Stromänderungen und gegenseitiger Induktivität der benachbarten Spulen
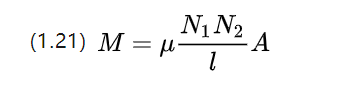
Der Koeffizient der gegenseitigen Induktivität von Materialien mit linearer Identität wird durch die obige Gleichung angenähert, die zeigt, dass die gegenseitige Induktivität von der Anzahl der Windungen der beiden Spulen gleichzeitig beeinflusst wird.
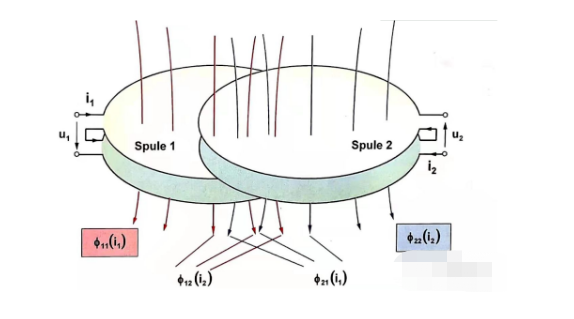
Wenn man den Widerstand außer Acht lässt und die Selbst- und Gegeninduktivität der beiden benachbarten Spulen untersucht, kann die Spannungsgleichung aus Abbildung 1.5 für Gleichstrommotoren aufgeführt werden
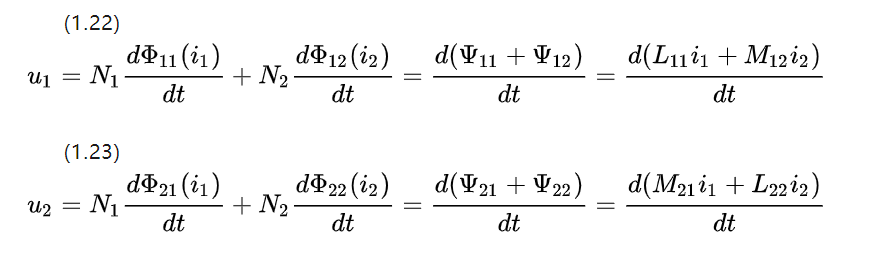
Da die Kopplungsteile die gleichen Materialparameter und die gleiche Form haben, sind die resultierenden Gegeninduktivitätskoeffizienten gleich M12=M21.
Die Größe der Kopplungsketten an jeder Spule ist also proportional zur Stromstärke an der entsprechenden Rotorwicklungsspule für einen Gleichstrommotor.
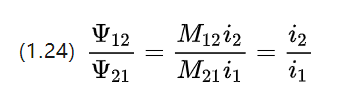
1,5-Ohm-Theorem für elektrische Energie und magnetische Kreise
In der weiterführenden Schule haben wir den Ohmschen Satz studiert, der besagt, dass der Widerstand eines Leiters das Verhältnis von Spannung und Strom an beiden Enden ist und dass es eine Formel zur Beschreibung des Widerstandsmaterials selbst gibt.
Q ist die Leitfähigkeit, die genau der Kehrwert des spezifischen Widerstands P ist und die Fähigkeit beschreibt, Strom zu leiten.
Neben dem angelegten Widerstand kann auch der Zusammenhang zwischen Spannung und Strom anhand des Leitfähigkeitsbildes beim Betrieb des Elektromotors beschrieben werden.
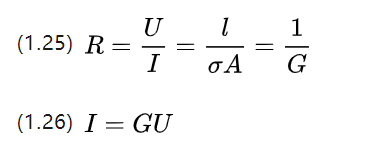
Untersuchen Sie nun die Stromstärke pro Flächeneinheit, d. h. die Stromdichte J = I/A e (e ist der Einheitsvektor), wobei die Stromdichte bei Wechselstrommotoren ein Vektor ist, der in die Richtung des Stroms zeigt.
Dies kann mit der Spannungsgleichung U=E.l und (1.25) kombiniert und in (1.26) umgeschrieben werden
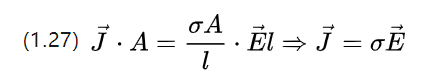
Die obige Gleichung beschreibt den Ohmschen Satz auf mikroskopischer Ebene, d. h. die Variation der Stromdichte entsprechend einer konstanten Feldstärke, die an den Leiter angelegt wird.
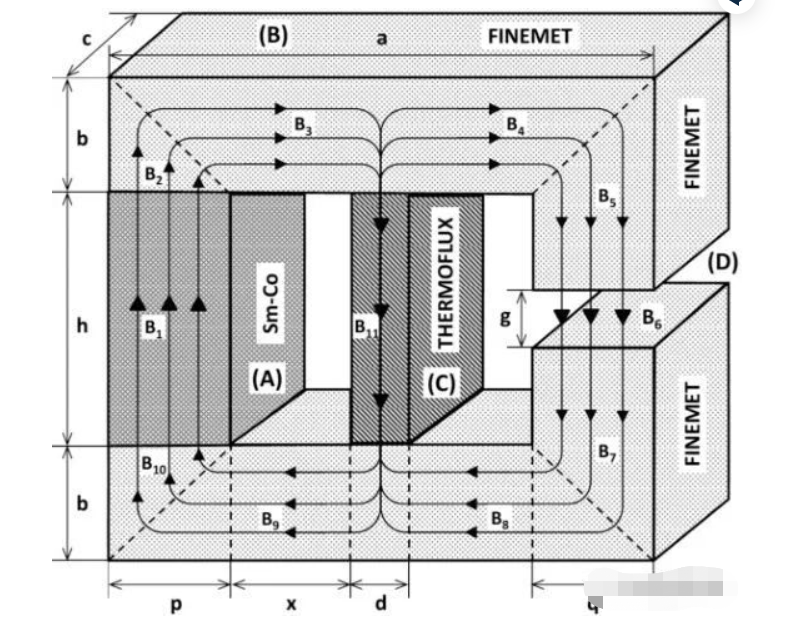
Lm ist die effektive Länge des magnetischen Flusses durch einen Abschnitt des Magnetkreises und A ist die entsprechende Flussfläche.
Die obige Gleichung ist der Widerstandsformel sehr ähnlich.
Verformen wir die Magnetowiderstandsformel noch einmal und wir können weiterhin erhalten
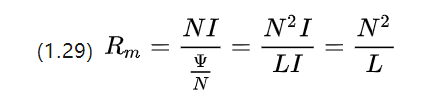
Es ist ersichtlich, dass der Magnetowiderstand in Einheiten tatsächlich der Kehrwert des Induktivitätskoeffizienten ist.
Wenn wir die Analogie zum Konzept der Leitfähigkeit fortsetzen, erhalten wir den magnetischen Leitwert A (magnetischer Leitwert, in [H] oder [Ωs]).
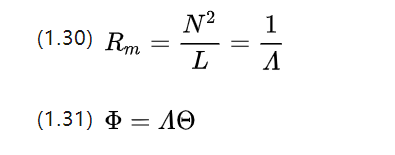
Im Schaltkreis finden wir die Differentialelemente für (1.26) und erhalten den mikroskopischen Ohmschen Satz. Was ist also der mikroskopische Ohmsche Satz, der dem magnetischen Kreis entspricht?
Wir können Gleichung (1.31) umschreiben und dabei beachten, dass der magnetische Fluss selbst eine Flussdichte B hat, die sich dann ergibt
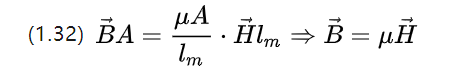
Der Ohmsche Satz des mikroskopischen Magnetkreises ist also Gleichung (1.10), und die magnetische Feldstärke darunter ist die Flussdichte, die sich aus der Magnetisierung eines konstanten Magnetfelds ergibt.
Die rechnerische Analyse der Reluktanz kann verwendet werden, um eine Mikroelementanalyse des Flusses im gesamten Motorwicklungspol, Kernteil und Zwischenluftspaltteil zu realisieren, wodurch eine diskrete Finite-Elemente-Analyse FEM (Finite-Elemente-Methode) realisiert werden kann. des gesamten Magnetkreises.
Es ist auch möglich, den Satz von Kirchhoff für die Schaltung im magnetischen Kreis anzuwenden, was sehr intuitiv und praktisch ist.
Gerne können Sie uns im Kommentarbereich weitere Informationen zu Elektromotoren mitteilen!
Bei Fragen zum Elektromotor wenden Sie sich bitte an den professionellen Elektromotor Hersteller In China wie folgt:

Dongchun Motor verfügt über eine breite Palette von Elektromotoren, die in verschiedenen Branchen wie Transport, Infrastruktur und Bauwesen eingesetzt werden.
Erhalten Sie umgehend eine Antwort.








